Model-View-Projection

Nov 2, 2024

9 mins read

Graphics
Graphics

2D Transformations

Scale

$$ S(s_x, s_y) = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Rotation

$$ R(\alpha) = \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Translation

$$ T(t_x, t_y) = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} $$

齐次坐标的最后一位为 0 表示方向或无穷远点

平移变换不会影响最后一位为 0 的坐标，因此这些坐标无法通过平移操作改变位置。

三维与二维变换同理

先平移再旋转与先旋转再平移得到的结果是不一样的

由此可推出矩阵乘法是不符合交换律

$$ A_n (\dots A_2 (A_1 (\mathbf{x}))) = A_n \cdots A_2 \cdot A_1 \cdot \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} $$

在齐次坐标中的矩阵变换计算中，运算顺序是从右到左，即最先应用的是最右边的矩阵，然后依次往左应用。

如果想绕着C点进行旋转

先平移到原点，然后再旋转，最后再平移回去

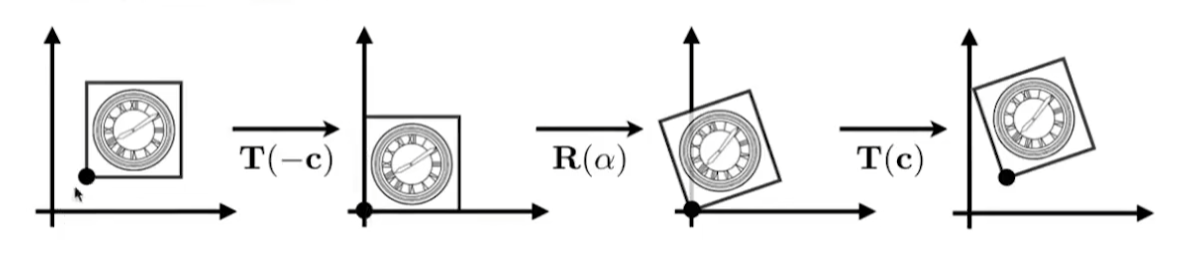
How to rotate around a given point C?

$$ T(c) \cdot R(\alpha) \cdot T(-c) $$

旋转矩阵（围绕 x, y, z 轴）

围绕 x 轴的旋转矩阵：

$$ R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$

围绕 y 轴的旋转矩阵：

$$ R_y(\alpha) = \begin{bmatrix} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$

围绕 z 轴的旋转矩阵：

$$ R_z(\alpha) = \begin{bmatrix} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$

透视投影矩阵的主要目的是通过将三维坐标缩放并转换为齐次坐标，将视锥体中的物体投影到二维平面上

  • zNear：近裁剪面的位置
  • zFar：远裁剪面的位置
  • l, r：视锥体左右边界 (aspect_ratio)
  • t, b：视锥体的上下边界
$$ M_{projection} =M_{ortho}×M_{\text{persp\_to\_Ortho}} $$

透视投影转正交矩阵为：

$$ M_{\text{persp\_to\_ortho}} = \begin{bmatrix} z_{\text{Near}} & 0 & 0 & 0 \\ 0 & z_{\text{Near}} & 0 & 0 \\ 0 & 0 & z_{\text{Near}} + z_{\text{Far}} & -z_{\text{Near}} \cdot z_{\text{Far}} \\ 0 & 0 & 1 & 0 \end{bmatrix} $$

正交投影矩阵为：

$$ M_{ortho} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} $$

缩放矩阵（缩放至[−1,1] 区间为2）和平移矩阵（移动到原点位置）

t = tan(angle / 2) * -zNear (因为右手定则z轴为负)

b = -t

r = t * aspect_ratio

l = -r

旋转矩阵的罗德里格斯公式

$$ R = I \cos \theta + (1 - \cos \theta)(\mathbf{k} \mathbf{k}^T) + \sin \theta \begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x & 0 \end{bmatrix} $$

其中：

  • I是单位矩阵。

  • kkT 是旋转轴的外积，表示旋转轴的投影矩阵。

  • 最后一项是旋转轴的叉积矩阵，表示垂直旋转轴的旋转分量。

作业0

给定一个点P=(2,1),将该点绕原点先逆时针旋转45◦，再平移(1,2),计算出 变换后点的坐标。（要求用齐次坐标进行计算）

编译

为方便之后的作业编写，本次作业要求使用cmake进行编译。

首先，编写好本次作业的程序main.cpp。 然后, 在 main.cpp 所在目录下，打开终端(命令行)，依次输入：

• mkdir build: 创建名为 build 的文件夹。

• cd build: 移动到 build 文件夹下。

• cmake ..: 注意其中’..’ 表示上一级目录，若为’.’ 则表示当前目录。

• make: 编译程序，错误提示会显示在终端中。

**• ./Transformation：**若上一步无错误，则可运行程序(这里的Transformation 为可执行文件名，可参照CMakeLists.txt 中修改)。

#include<cmath>
#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Dense>
#include<iostream>

int main(){
    // init point
    Eigen::Vector3f p(2.0f, 1.0f, 1.0f);

    // rotate and transformation matrix
    // x' = xcos - ysin
    // y' = xsin + ycos
    // x' = x + tx
    // y' = y + ty
    Eigen::Matrix3f R, T;
    // cos45 = sin45 = sqrt(2) / 2
    float ftheta = sqrt(2.0f) / 2;
    R << ftheta, -ftheta, 0,
         ftheta, ftheta, 0,
         0, 0,1.0f;

    T << 1.0f, 0, 1.0f,
         0, 1.0f, 2.0f,
         0, 0, 1.0f;

    p = R * p;
    std::cout << "After Rotate \n";
    std::cout << p << std::endl;

    p = T * p;
    std::cout << "After Transformation \n";
    std::cout << p << std::endl;

    return 0;
}

附件

pa0.pdf

CMakeLists.txt

作业1

模型变换矩阵

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
    float rotation_angle_radian = rotation_angle * MY_PI / 180;
    Eigen::Matrix4f rotation;
    rotation << cos(rotation_angle_radian), -sin(rotation_angle_radian), 0, 0,
                sin(rotation_angle_radian), cos(rotation_angle_radian), 0, 0,
                0, 0, 1, 0,
                0, 0, 0, 1;
    model = rotation * model;

    return model;
}

投影变换矩阵


Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar)
{
    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

    float eye_fov_radian = eye_fov * MY_PI / 180;
    float t = tan(eye_fov_radian / 2) * abs(zNear);
    float r = t * aspect_ratio;
    float b = -t;
    float l = -r;

    Eigen::Matrix4f translation;
    translation << 1, 0, 0, -(r + l) / 2.0f,
                   0, 1, 0, -(t + b) / 2.0f,
                   0, 0, 1, -(zNear + zFar) / 2.0f,
                   0, 0, 0, 1;

    Eigen::Matrix4f scale;
    scale << 2.0f / (r - l), 0, 0, 0,
             0, 2.0f / (t - b), 0, 0,
             0, 0, 2 / (zNear - zFar), 0,
             0, 0, 0, 1;

    projection = scale * translation;
    Eigen::Matrix4f M_persp_ortho;
    M_persp_ortho << zNear, 0, 0, 0,
                     0, zNear, 0, 0,
                     0, 0, zNear + zFar, -zFar*zNear,
                     0, 0, 1, 0;
                     
    projection = projection * M_persp_ortho;
    return projection;
}

任意轴旋转矩阵罗德里格斯旋转公式

Eigen::Matrix4f getRotation(Vector3f axis, float angle){
    float rotation_angle_radian = angle * MY_PI / 180;
    Eigen::Matrix3f I = Eigen::Matrix3f::Identity();
    Eigen::Matrix3f N;
    N << 0, -axis(2), axis(1),
         axis(2), 0, -axis(0),
         -axis(1), axis(0), 0;
    Eigen::Matrix3f r3 = cos(rotation_angle_radian) * I
    + (1 - cos(rotation_angle_radian)) * (axis * axis.transpose())
    + sin(rotation_angle_radian) * N;
    Eigen::Matrix4f rotation = Eigen::Matrix4f::Identity();
    rotation.block(0, 0, 3, 3) << r3;
    return rotation;
}

附件

Sharing is caring!