光栅化Rasterize

Dec 3, 2024

15 mins read

Graphics
Graphics

屏幕坐标系

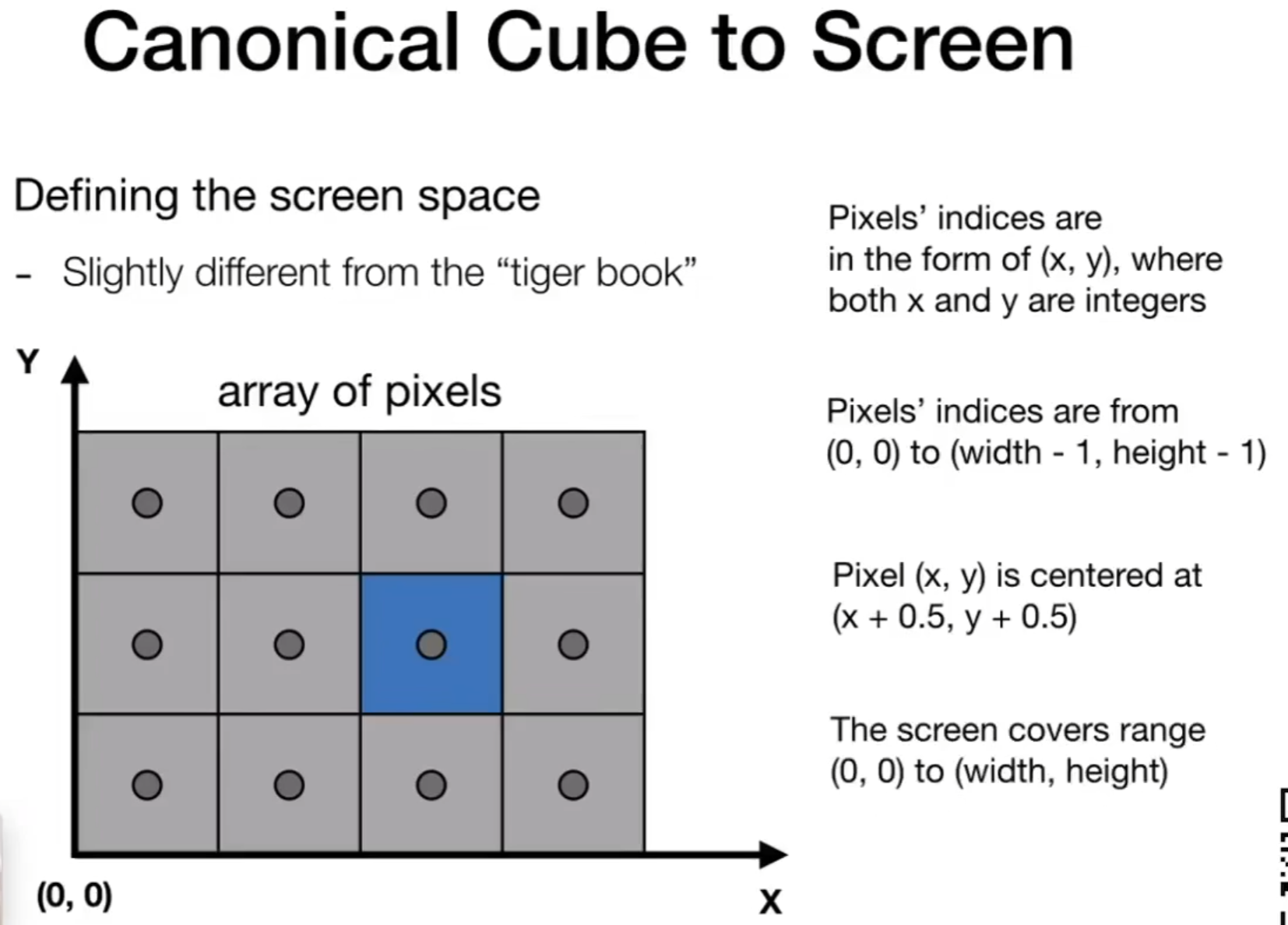
屏幕空间 - 在屏幕上建立一个坐标系

屏幕的左下角是原点（0，0） 向上是Y 向右是x

Screen

视口变换

要做的事：[-1, 1]^3映射到屏幕上

其中：width 和 height 是屏幕或视口的宽度和高度

在标准化设备坐标中，3D物体的投影结果被限制在 (−1,−1)到 (1,1) 的范围：

  • (−1,−1) 代表左下角
  • (1,1) 代表右上角
  • 这是一个对称的正方形坐标系，中心点是 (0,0)

我们需要将这个范围映射到屏幕坐标系：

  • 左下角是 (0,0)，右上角是 (width,height)
$$ M_{viewport} = \begin{pmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2}\\ 0 & \frac{height}{2} & 0 & \frac{height}{2}\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$

光栅显示设备

  • 示波器（曾经做过的物理实验）和早期显示器相同原理

​ 阴极射线管 电子经过加速穿过显示设备 发生偏转 就可以看到CRT屏幕 （Cathode Ray Tube）

​ 隔行扫描（第一帧记录奇数行 下一帧记录偶数行） 直到现在还在一些视频压缩中使用 缺点：画面撕裂

  • 帧缓冲区（FrameBuffer）

​ 是内存中的一块区域，存储显示在屏幕上的像素数据并映射到屏幕上

  • 液晶显示器（LCD）

​ 计算器、手机等，通过液晶扭曲，改变光的振动方向

  • 发光二极管（LED）

  • ElectroPhoretic（电子墨水屏）

​ 例如Kiddle，缺点：刷新率很低

Question：为什么三角形被图形学广泛应用？

Answer：

  • 三角形是最基础的多边形 可以拼凑成多边形
  • 三个点一定是平面的 内部没有凹陷
  • 三角形的几何计算效率高

光栅化方法

采样

1.采样：采样每个在三角形内部像素点的中心

for (int x = 0; x < xmax; x++)
    for (int y = 0; y < ymax; y++)
        image[x][y] = inside(tri, x + 0.5, y + 0.5);

inside函数判断像素点中心是否在三角形内部，如果在返回1，反之0

判断点是否在三角形

2.判断点是否在三角形

向量叉乘 如果三个叉乘结果都＞0 / < 0，则在三角形内

光栅化计算加速（三角形遍历方法）

3.光栅化计算加速（三角形遍历方法）

由于三角形所涉及到的区域是能够确定的，所以没必要从整个视口大小的像素范围遍历

  • 包围盒遍历

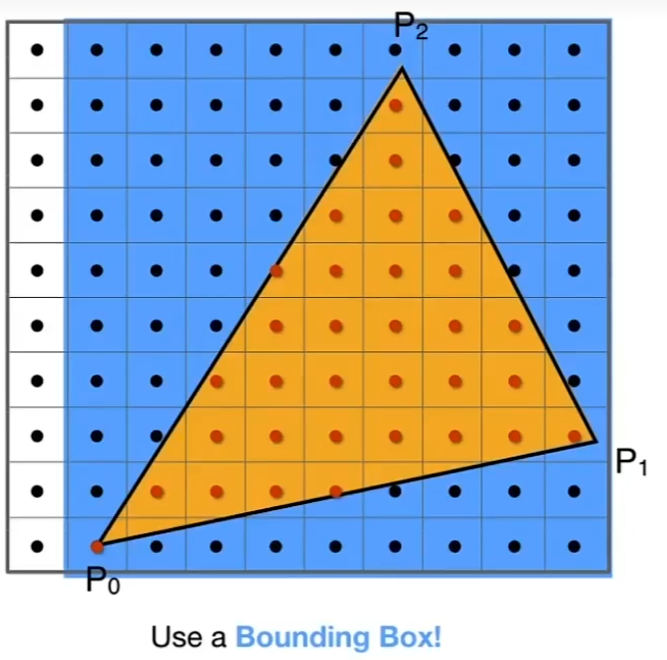
    BoundingBox

    包围盒的大小如下

    $$ [min(x_{p0}, x_{p1},x_{p2}), max(x_{p0}, x_{p1},x_{p2})] \times[min(y_{p0}, y_{p1},y_{p2}), max(y_{p0}, y_{p1},y_{p2})] $$

  • 增量三角形遍历

ITT

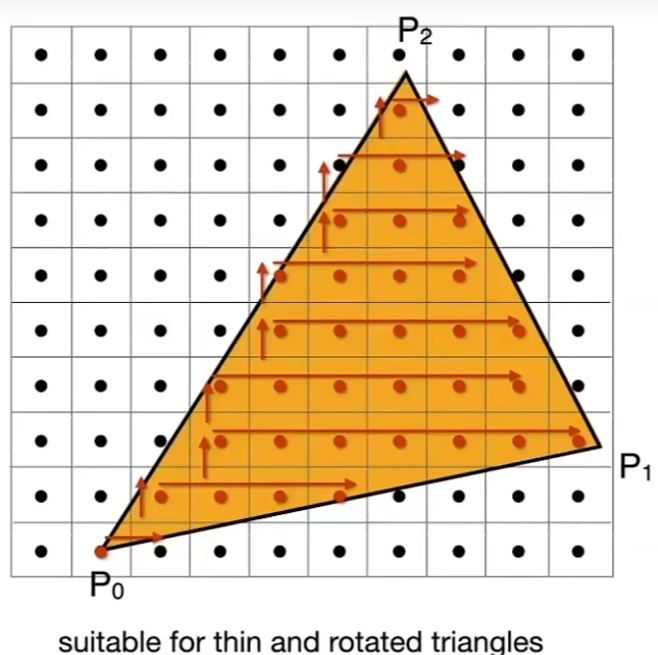
通过计算三角形边的直线方程 利用直线生成布雷森汉姆算法（Bresenham algorithm），可以确定三角形每一行的左边界和右边界

抗锯齿 / 反走样（Anti Aliasing）

锯齿（Aliasing）

导致的原因：采样率不够高。

通常采用的反走样的方法是，先对图形进行模糊处理然后在进行采样

傅里叶级数展开

一切函数都可以被写成一系列正弦和余弦函数的线性组合加上一个常数项

让函数无限接近于图像

$$ f(x) = \frac{A}{2} + \frac{2Acos(t\omega)}{\pi}+\frac{2Acos(3t\omega)}{3\pi}+\frac{2Acos(5t\omega)}{5\pi}+... $$

频率与采样

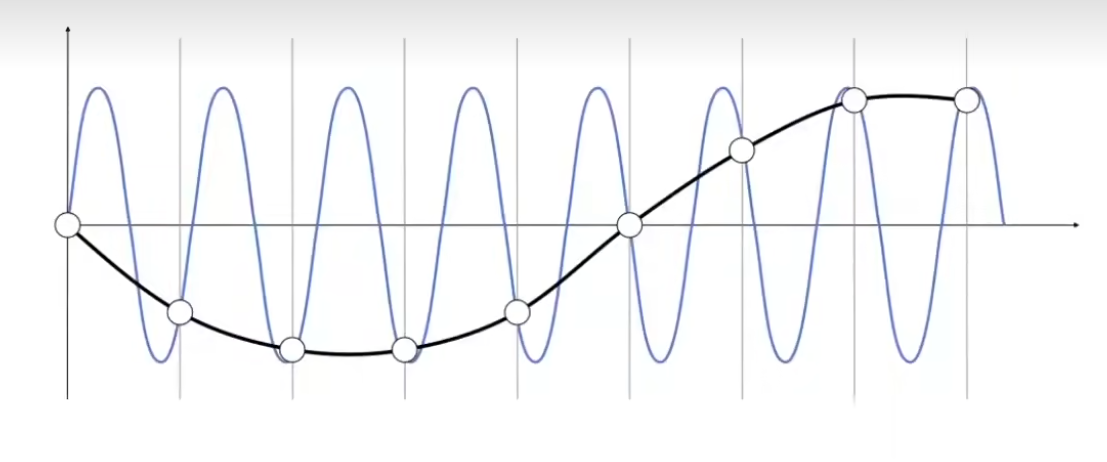
如图，如果函数频率不断增加，而采样频率相同，采样结果就会出现偏差，就会产生走样现象

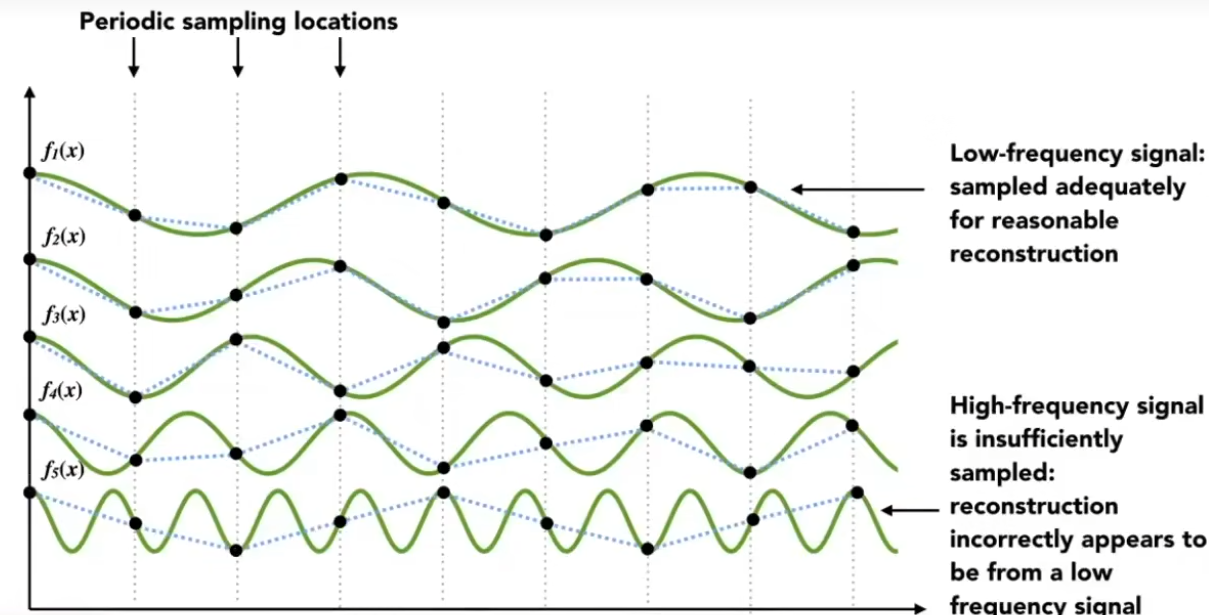
frequency_sampling

而下图会发现，两种截然不同的两种函数（黑线和蓝线）却能得出相同的结果，无法区分来自哪个函数，就会出现走样现象

twoFx

滤波

去掉一些在频率上特定的频率

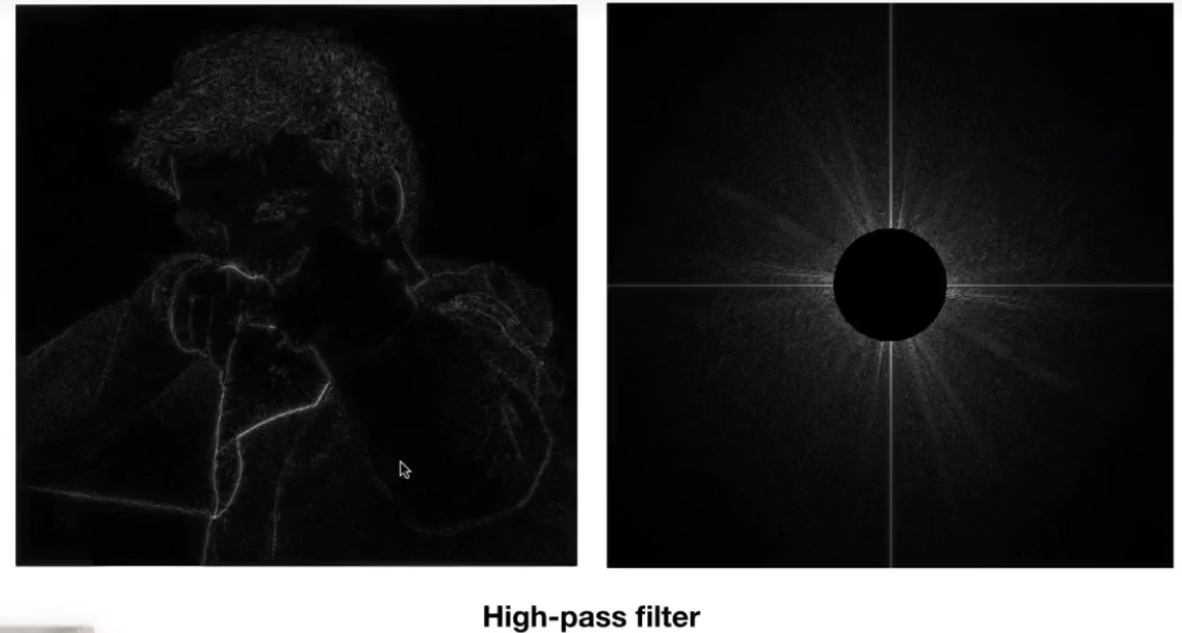
  • 高通滤波（High-Pass Filter）

    可以通过高频信号，过滤低频信号，然后通过傅里叶变化，高频信号表示物体内容上的边界信息。

    原因：傅里叶变换前物体的边界，颜色变化剧烈，会产生剧烈变化的信号，剧烈变化会产生高频信号。

    highPassFilter

  • 低通滤波（Low-Pass Filter）

    可以通过低频信号，过滤高频信号，经过傅里叶变换的图像中所有高频信号去掉，留下低频信号，在经过傅里叶变换就会得到下面的图像。

    图片模糊了是因为过滤掉了表示图像边界的高频信号

    lowPassFilter

  • 带通滤波（Band-Pass Filter）

    允许限定频段通过，通常是将一张图片经过傅里叶变换得到频域，然后去掉高于限定的最高频和低于限定的最低频信号。

卷积

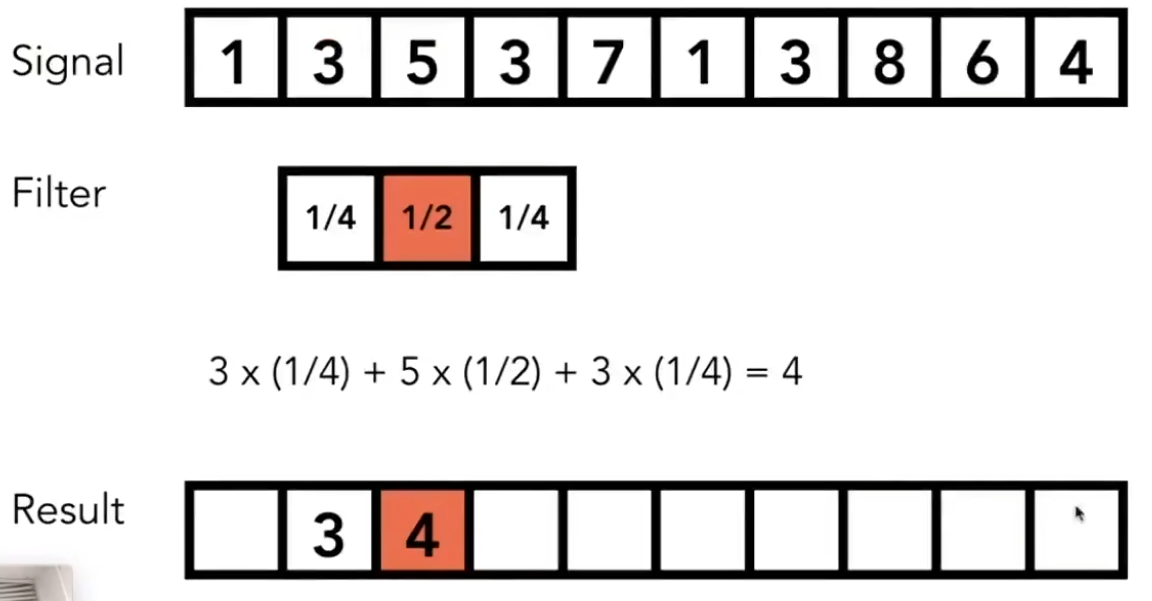
卷积就是定义一个滤波器，滤波器也称为卷积核，这个滤波器可以是一维数组/二维数组。使用滤波器对原信号挨个进行处理，将处理结果写进与原数据大小相同的容器中。

第一个信号和最后一个信号要特殊处理一下，第一个信号，最左边并没有信号对应卷积核的第一个值。对于缺省的信号需要自动补零。第一个信号取得的31的信号值分别为0,1,3，然后进行卷积操作，得到的结果为 (0 * 1/4) + (1 * 1/2) + (3 * 1/4) = 1.25

Convolution

时域上的卷积相当于频域上的乘积

采样与频域

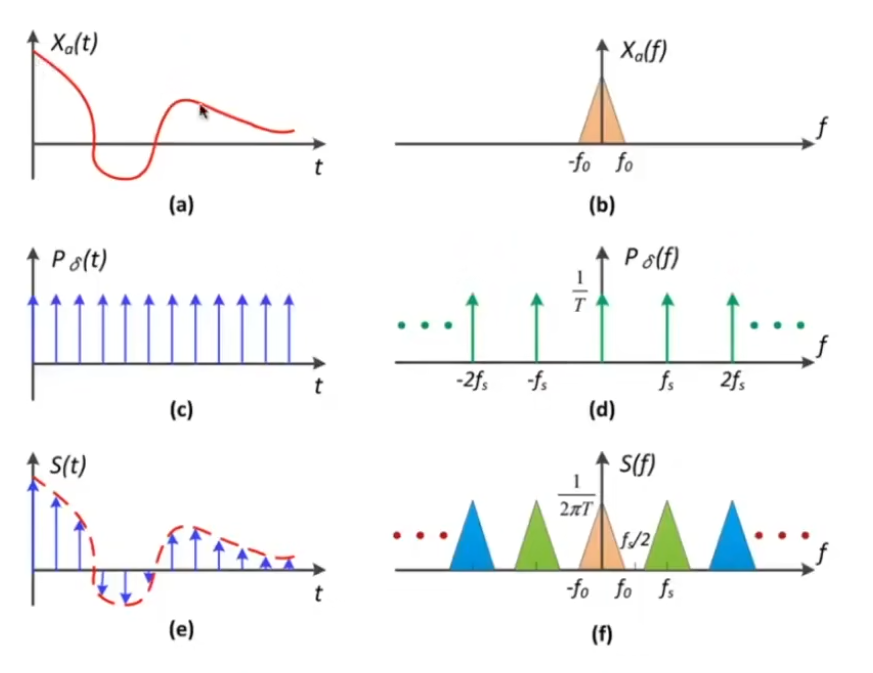
采样就是在重复原始信号的频谱

a是连续函数（信号），b是该函数经过傅里叶变化后在频域上的体现

c是采样函数，d是采样函数在频域上的体现

由于时域上的卷积相当于频域上的乘积

使用a函数与c函数相乘 = e函数（采样的结果） 等价于 b卷积d = f

sampling

走样

采样时复制粘贴频谱发生混叠

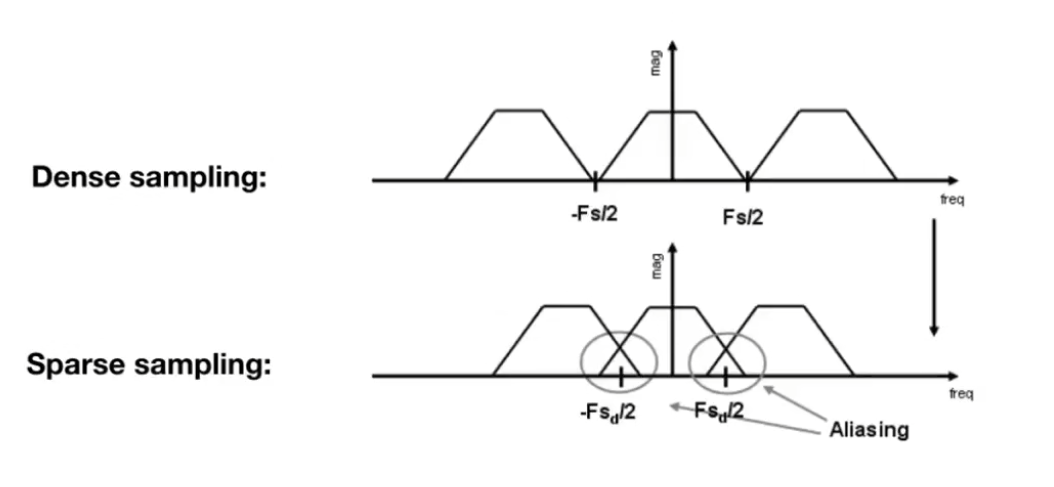
Aliasing

反走样方法

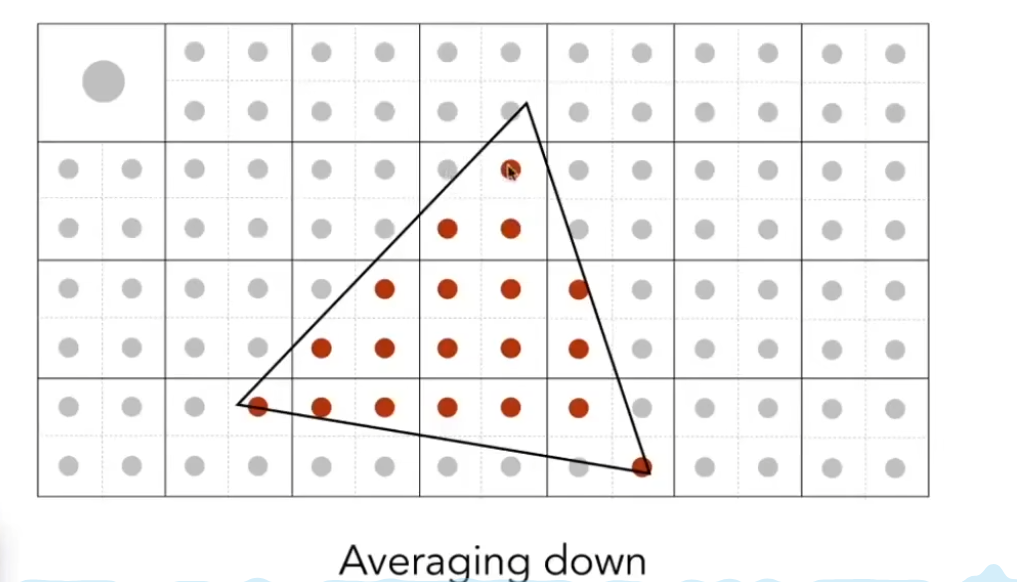
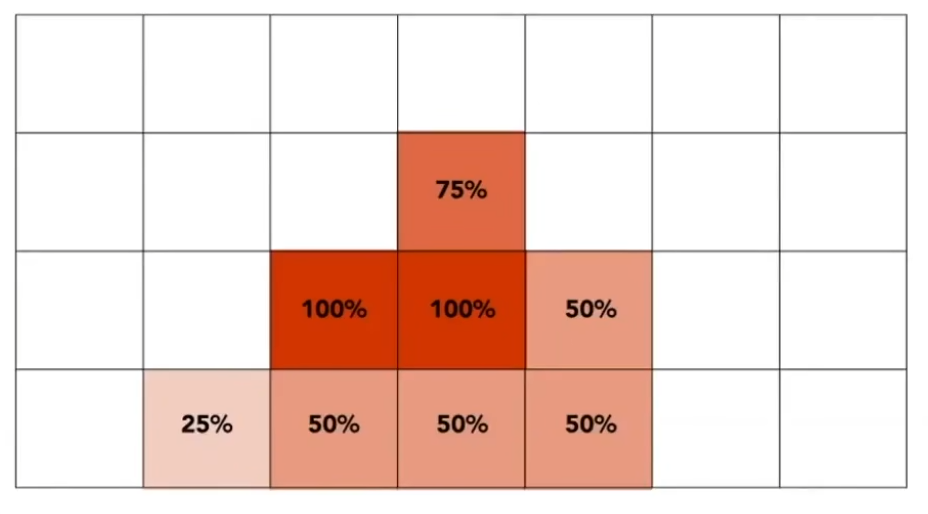
多重采样MSAA

取更多的点实现反走样 把一个像素划分成很多个小的像素 同样每个小像素也有中心点

增加采样点 没有提高屏幕分辨率

MSAA1

MSAA2

快速近似抗锯齿FXAA

和采样无关，在图像层面做的处理，处理过程是先找到三角形的边界，把有锯齿的边界替换为没有锯齿的边界，而且处理起来非常快。

时间抗锯齿TAA

在渲染过程中，TAA 会使用前几帧的图像信息进行参考，并结合当前帧的图像数据。这意味着它不仅仅依赖于当前帧的像素，而是通过对比多个帧之间的像素位置、颜色和深度来进行抗锯齿处理。

深度学习超级采样DLSS

依赖深度学习，使用低分辨率(比如1080p)渲染图象，为了尽量减少计算负担，提高帧率，然后使用深度学习生成高分辨率的图像（智能补全）。

MSAA和SSAA区别

特性 SSAA MSAA
原理 在更高分辨率下渲染整个场景，然后缩放回目标分辨率，平均化采样值。 对几何边缘的像素执行多点采样，仅对边缘进行处理，不对整个场景进行超采样。
性能消耗 非常高，因为整个帧缓冲区都需要更高分辨率进行渲染。 相对较低，因为只对几何边缘的像素进行多次采样。
效果 更高质量，可以处理所有类型的锯齿（包括几何边缘和纹理细节）。 主要处理几何边缘锯齿，对纹理锯齿和后处理效果（如透明对象）支持有限。
使用场景 适合需要高画质的离线渲染（如电影、静态图像）。 更适合实时渲染（如游戏），在画质和性能之间取得平衡。

作业

hw

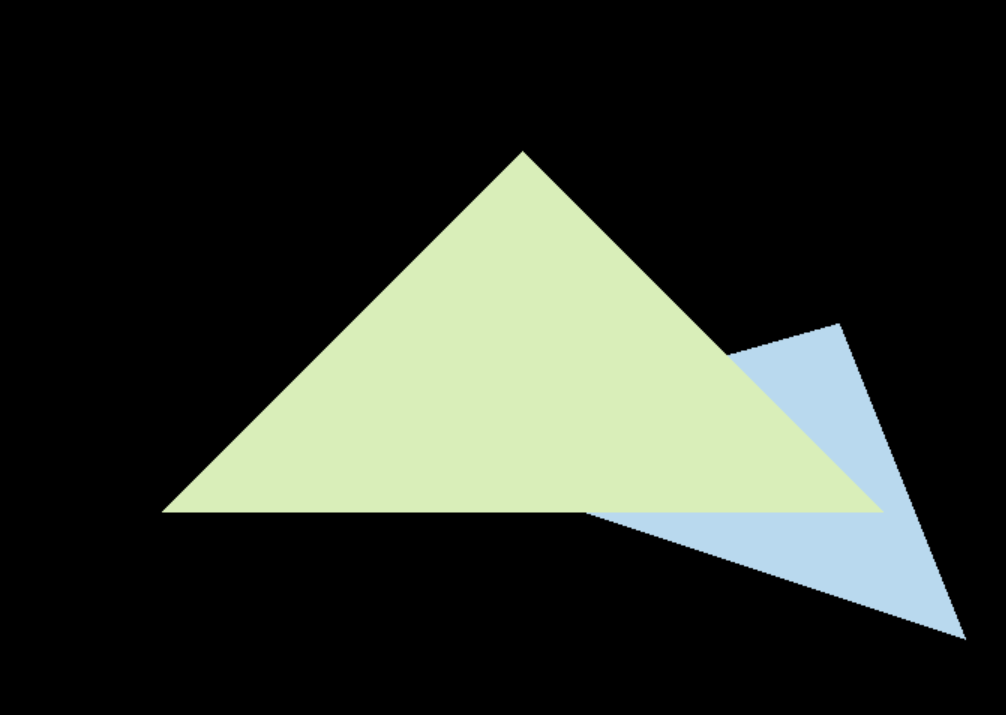
void rst::rasterizer::rasterize_triangle(const Triangle& t)
{
    auto v = t.toVector4();
    int minx, maxx, miny, maxy;
    minx = std::min(v[0].x(), std::min(v[1].x(), v[2].x()));
    miny = std::min(v[0].y(), std::min(v[1].y(), v[2].y()));
    maxx = std::max(v[0].x(), std::max(v[1].x(), v[2].x()));
    maxy = std::max(v[0].y(), std::max(v[1].y(), v[2].y()));
    
    // 遍历包围盒中每个像素
    for (int x = minx; x <= maxx; x ++)
    {
        for (int y = minx; y <= maxy; y++)
        {
            // 检查包围盒中的像素点是否在三角形内部
            if (insideTriangle(x, y, t.v))
            {
                // 求深度插值 重心坐标的权重系数
                float alpha, beta, gamma;
                std::tie(alpha, beta, gamma) = computeBarycentric2D(x + 0.5, y + 0.5, t.v);
                float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                z_interpolated *= w_reciprocal;
                // rasterization
                // 计算当前像素在深度缓冲区中的索引
                auto ind = get_index(x, y);
                if (z_interpolated < depth_buf[ind])
                {
                    depth_buf[ind] = z_interpolated;
                    Vector3f point = Vector3f((float)x, (float)y, z_interpolated);
                    Vector3f color = t.getColor();
                    set_pixel(point, color);
                }
            }
        }
    }
}

static bool insideTriangle(float x, float y, const Vector3f* _v)
{
    // TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]
    //Vector3f P(x + 0.5f, y + 0.5f, 1.0f);
    Vector3f P(x, y, 1.0f);

    const Vector3f& A = _v[0];
    const Vector3f& B = _v[1];
    const Vector3f& C = _v[2];

    Vector3f AB = B - A;
    Vector3f BC = C - B;
    Vector3f CA = A - C;

    Vector3f AP = P - A;
    Vector3f BP = P - B;
    Vector3f CP = P - C;

    float z1 = AB.cross(AP).z();
    float z2 = BC.cross(BP).z();
    float z3 = CA.cross(CP).z();

    return (z1 > 0 && z2 > 0 && z3 > 0) || (z1 < 0 && z2 < 0 && z3 < 0);
}

Sharing is caring!