Shader

Dec 16, 2024

16 mins read

Graphics
Graphics

Z-Buffer(深度缓存）

用来处理可见性问题，即确定每个像素最前层物体。

Frame Buffer(帧缓冲区：用于存储最终图像数据)、Depth Buffer（深度缓冲区：判断哪些物体在前，哪些物体被遮挡）

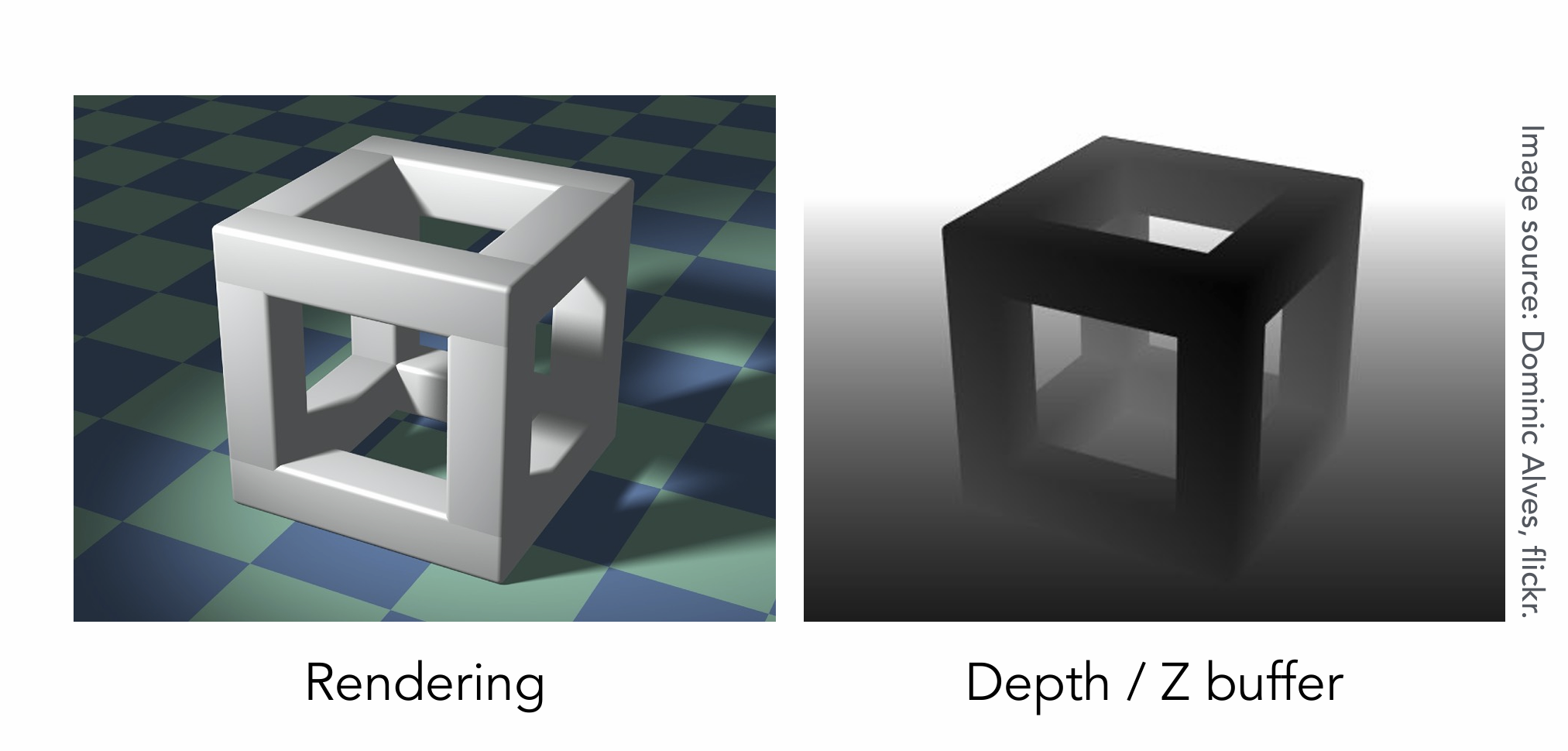
Z-buffer

工作原理：近处是更黑的，远处是发白的。

Z-Buffer处理不了透明物体，透明物体需要特殊处理。

Z-Buffer Algorithm

code

Z-BufferAlgorithm

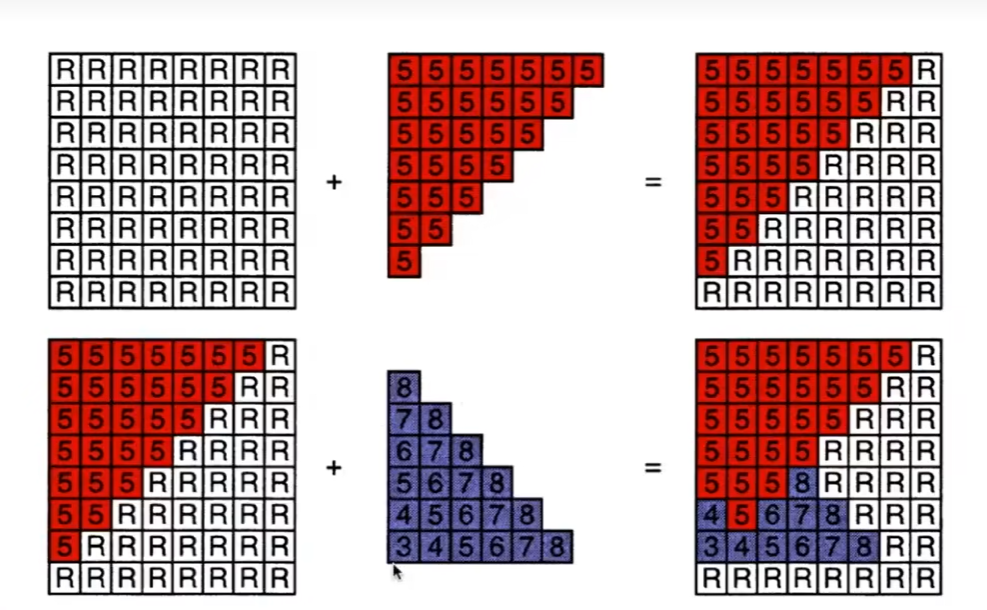
R代表无穷大，如果有三角形，就覆盖掉这些无穷大的像素

新的三角形深度是8 肯定要被原本三角形深度5所遮挡 所以就忽略它

如果新的三角形离的更近 更新这个像素对应的深度值

Z-Buffer复杂度 - O(n)

**Question：**为什么排序n个三角形是在线性的时间？

**Answer：**其实它不是排序，只是在对每个像素一直求最小值。

Shader

定义：对不同的物体应用不同材质的过程

物体在经过MVP（模型、视图、投影矩阵变换）、ViewPort之后现在我们会得到一系列旋转的立方体

需要对他做着色（Shading）

Blinn-Phong 反射模型

Blinn-Phong 反射模型是计算光照和表面反射的常用模型。它将光照分为三部分：

  • 漫反射（Diffuse Reflection）：表示光照与物体表面相互作用后，光线在不同方向上散射的现象，通常效果比较均匀，不会有明显的亮点。
  • 镜面反射（Specular Highlights）：表示光线被物体表面镜面反射的部分，产生亮光点，通常依赖于视角与光源方向的关系，产生较强的高光效果。
  • 环境光照（Ambient Lighting）：表示全局环境中的光照，通常是一个常量，作用于整个场景，不依赖于具体的物体或光源。

diffuse reflection

通常假设反射光是一个半球，并计算每个着色点（shading point）接收到的能量。漫反射的强度与光照方向和表面法线之间的夹角有关。

Lambert‘s cosine law：描述漫反射光照强度与光照方向和法线之间夹角的关系，公式如下：

$$ L_{d}=k_{d}\left(I / r^{2}\right) \max (0, \mathbf{n} \cdot \mathbf{l}) $$ $$ L_d:漫反射分量（反射光强度）\qquad k_d:漫反射系数（物体表面材质的属性）\qquad I:光源强度\qquad r:光源到表面点的距离 \qquad n:法线方向 \qquad l:光源方向 $$

注意：漫反射不考虑其他物体的影响，只关注当前着色点的表面法线与光照方向的关系。

Specular Highlights

v和R足够接近的时候，会看到高光，其中v是观测方向，R是光线反射方向。

实际上是n法线方向和h半程向量很接近，利用平行四边形法则，可以求v+l向量，再求单位向量就是半程向量h。

镜面反射光的公式

$$ L_{s}=k_{s}\left(I / r^{2}\right) \max (0, \mathbf{n} \cdot \mathbf{h})^p $$

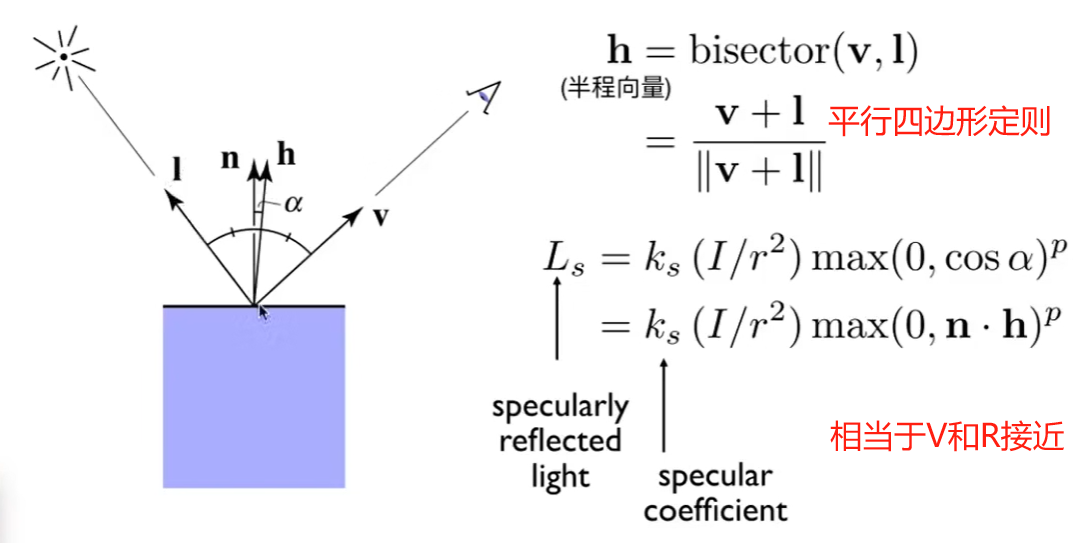
halfvector

高光非常亮，且集中在一个很小的角度里，所以要有指数，将角度范围缩小，高光就会越来越小。

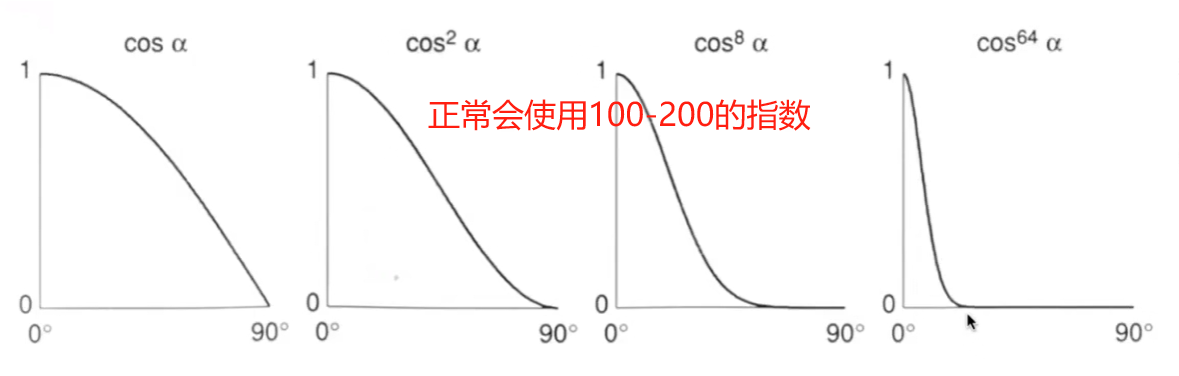
specular02

Ambient Lighting

环境光

$$ L_{a}=k_{a}I_{a} $$

Blinn-Phong Reflection

$$ L=L_{a}+L_{d}+L_{s} $$

Problem of Blinn-Phong

problem

ShadingFrequency

shadingFrequencies

Phong shading（每个像素进行着色）

当几何模型的面数不断增加，着色频率也会增加，也可以使用FlatShading，但是取决于具体的物体，因为模型比较复杂的话，反倒可能会用phong shading会更好，但是大多数情况，选择phong shading是不会错的。

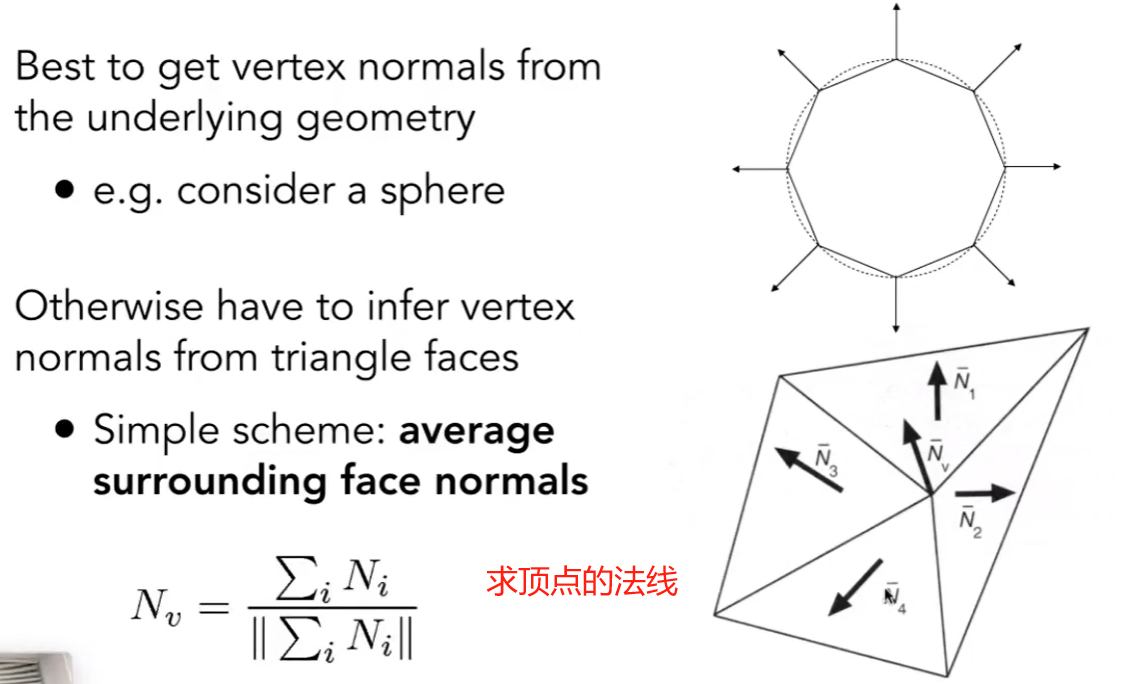
逐顶点求法线方向

当你知道一个模型对应的是什么物体的时候，你会通过下图（比如说有一个球形物体，和模型之间的接触的法线方向）

但是事实上你不知道模型是什么样的物体，于是只能通过计算每个平面的法线的平均值得到该点的法线方向，求加权平均值可能会得到更好的结果（面更大的求更大占比的法线方向向量），所有法线都要归一化。

vertexNormal

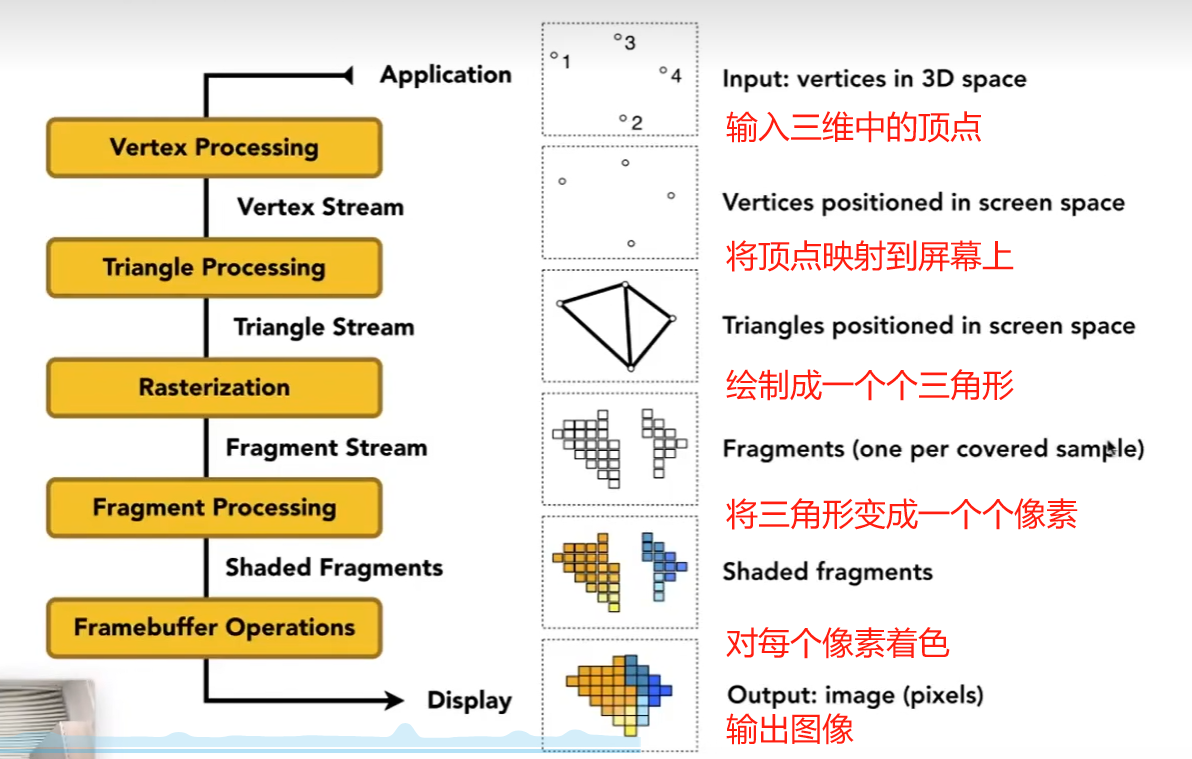
Graphics Pipeline

Pipeline

Shader概念

  • shader是写一个通用的程序，只需要管一个像素怎么运作
  • 如果操作一个顶点顶点着色器，如果操作一个像素像素（片源）着色器

分享一个网站Shadertoy BETA

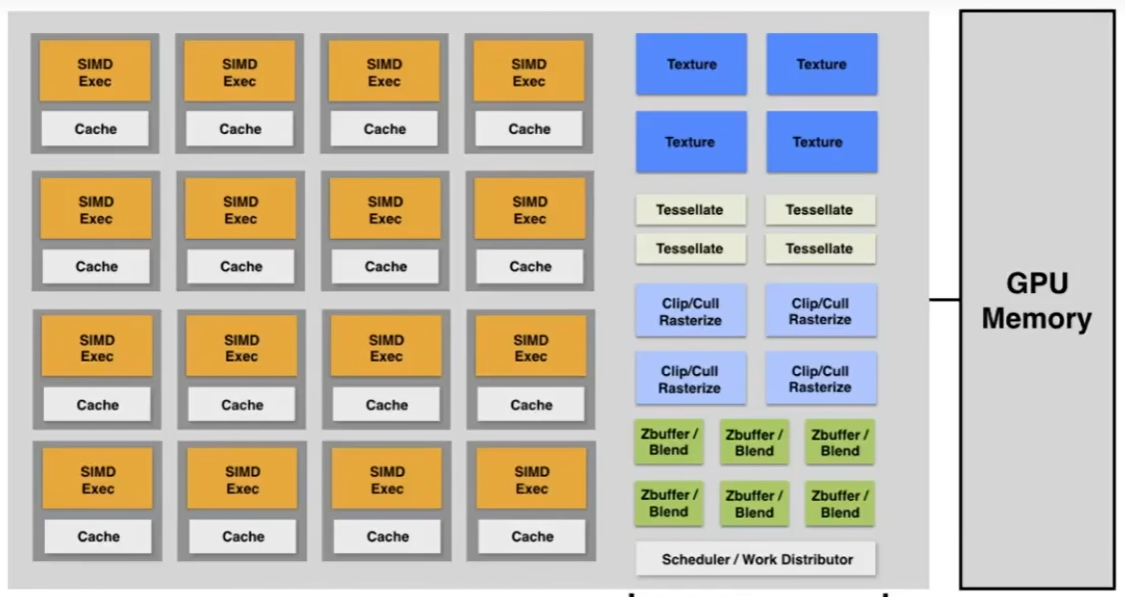
GPU

GPU 有成百上千个核心，这些核心被分为不同的小组，每一组可以执行不同 / 相同的人物，GPU的并行架构为处理大规模的相同类型操作而设计。

核心的数量 = 并行的数量，GPU并行度的速度远超过CPU的几十倍。

SIMD(Single Instruction, Multiple Data)是一种并行计算技术，它通过向量寄存器存储多个数据元素，并使用单条指令同时对这些数据元素进行处理，从而提高了计算效率。

gpu

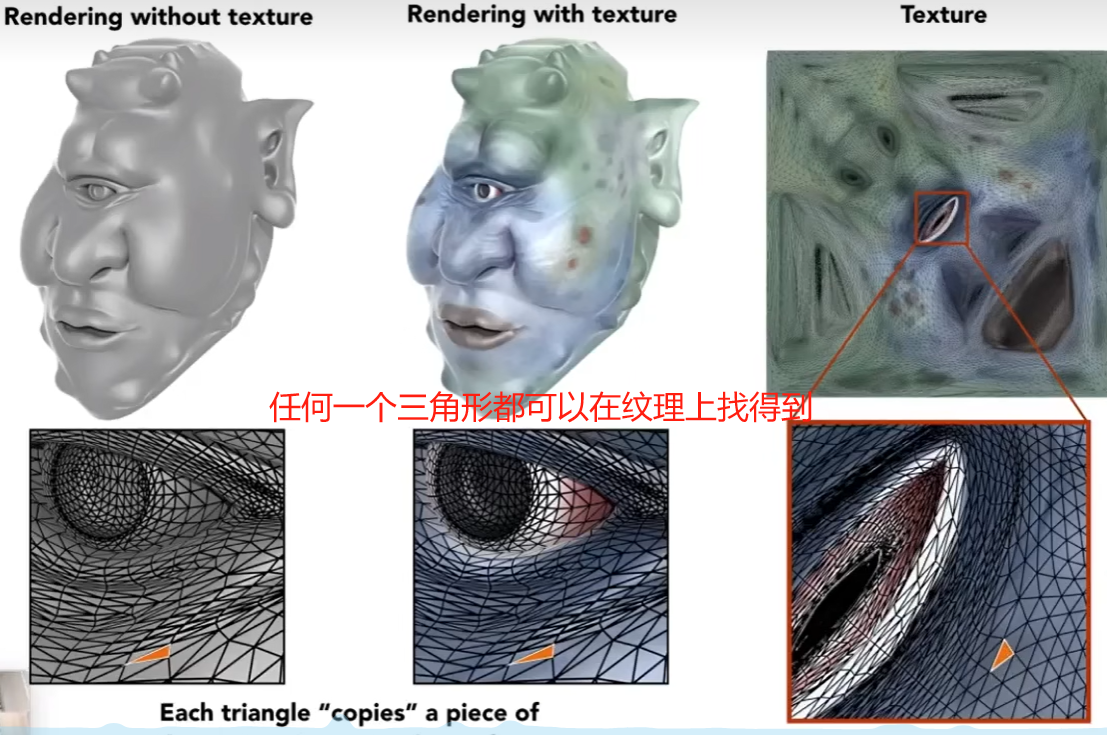
Texture

比如说我们对一个物体求它在灯光下的漫反射，但是这个物体的材质是不同的，这个物体表面有不同的颜色，呢么它的漫反射系数也是不同的。所以我们需要知道物体的表面信息，引出纹理。

将一个三维物体贴到一个二维的平面。

texture

纹理的坐标系通常使用 U, V 来表示，横轴 U，纵轴 V。通常 UV 的范围是 [ 0, 1 ] 之内。

重心坐标

用重心坐标在三角形内部做任何形式的插值

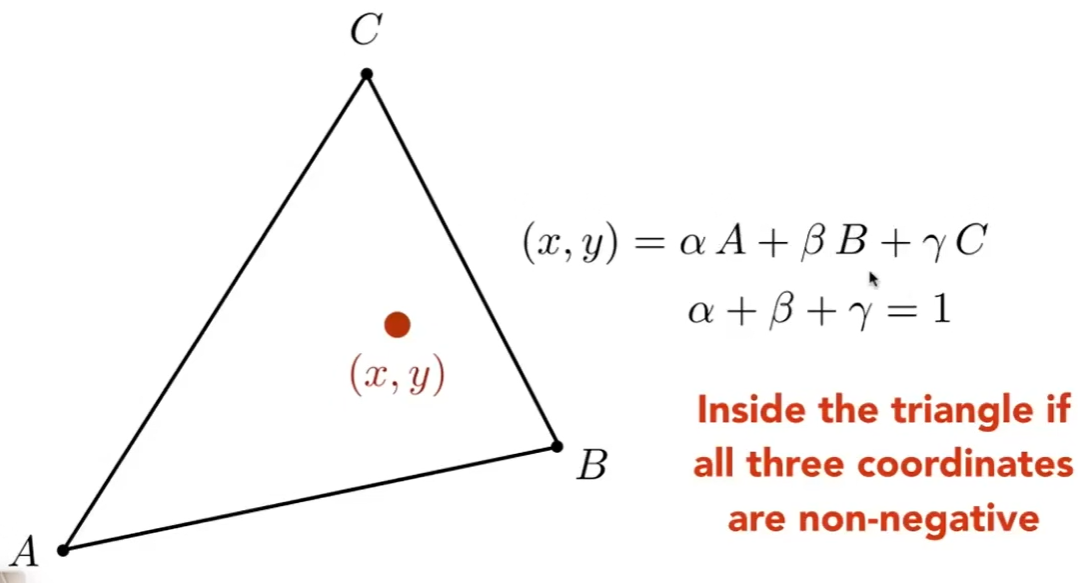
coordinate

A点的重心坐标是（1，0，0） 因为αA+βB+γC = A

如果任意一点，它的中心坐标如下

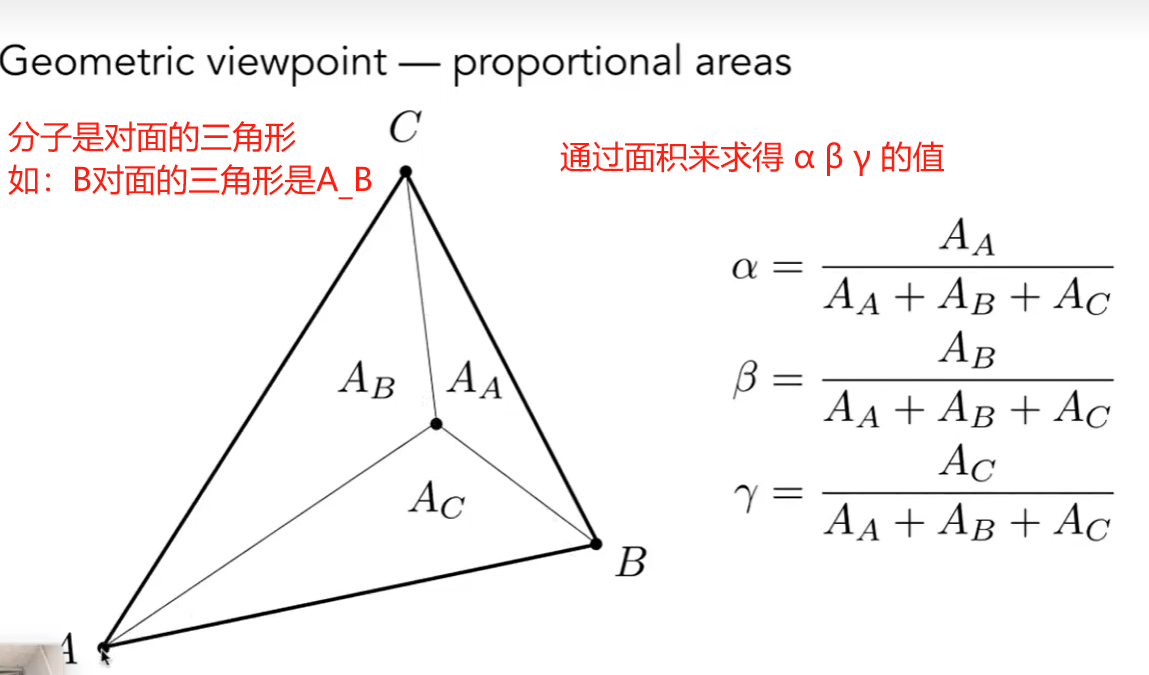
coordinate02

注意：但是需要在三维中求重心坐标，如果在投影之后再求重心坐标，呢么结果会不准确，因为在投影前后的重心坐标从三维变二维是会发生变化的。

Texture Magnification（纹理映射）

纹理过小时引发的问题

比如说将一张100*100 分辨率的纹理贴图应用在500*500的屏幕上，必然会走样，因为屏幕上好几个像素点对应纹理UV坐标都是一样的，那么会变成低分辨率的图像，所以应该怎么做？

Bilinear Interpolation双线性插值

通过两次线性插值，来缓解走样的现象。

![Bilinear Interpolation](/images/Graphics/Shader/Bilinear Interpolation.png)

Bicubic 双三次插值

取周围16个像素，比Bilinear运算量大，但是带来了更好的结果。

Question：是否纹理大结果会更好？

Answer：No，反而麻烦会更大，由于屏幕空间一个点会对应纹理贴图中一大片点，所以会得到远处的摩尔纹和近处的锯齿（走样）。

Solution：一种直观的解决方法就是Supersampling（超采样），如果一个像素点不足以代表一个区域的颜色信息，那么便把一个像素细分为更多个小的采样点。但是代价十分的高，计算量特别巨大。

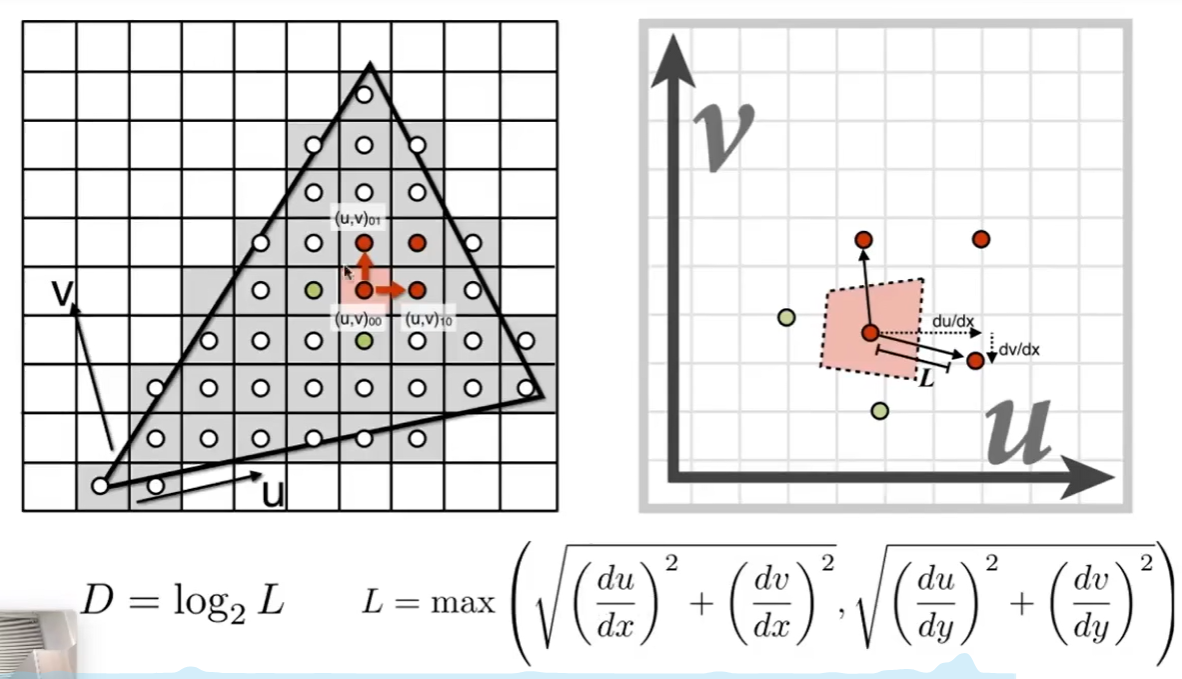
Mipmap 范围查询

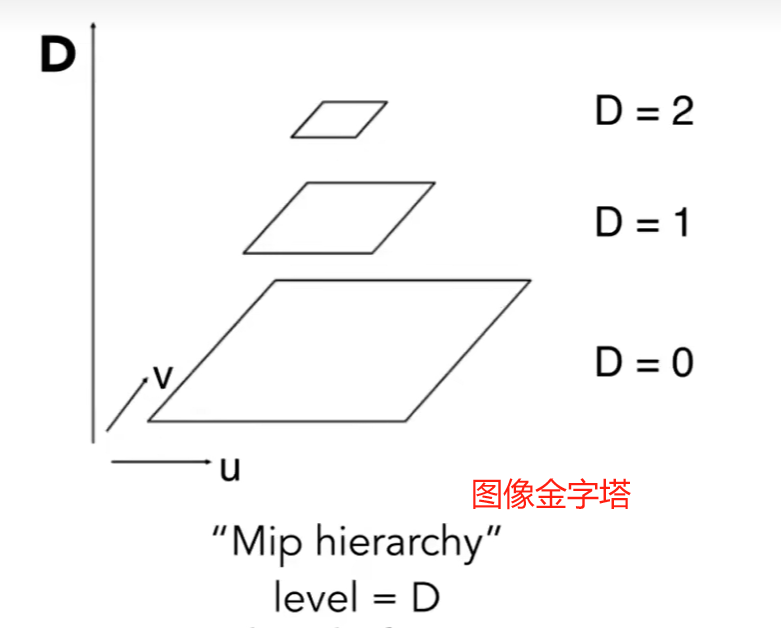
mipmap

通过设置不同的Level值来查询不同精度的纹理。Level值越大像素点被合并的越少

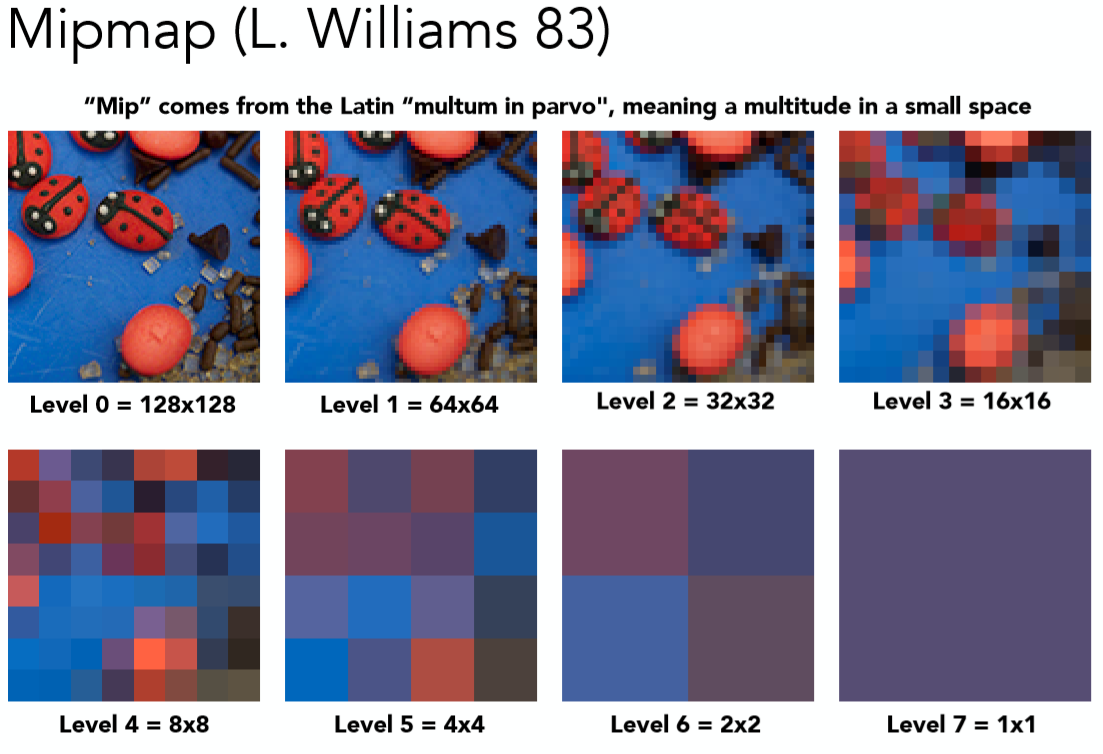
mipmap02

mipmap03

作业

基于包围盒的光栅化，用三角形的重心坐标对颜色、法线、纹理坐标做插值。将插值传递给fragment_shader_payload，调用 fragment_shader 计算最终像素颜色

void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array<Eigen::Vector3f, 3>& view_pos) 
{
    auto v = t.toVector4();

    int min_x = std::min(std::min(v[0].x(), v[1].x()), v[2].x());
    int min_y = std::min(std::min(v[0].y(), v[1].y()), v[2].y());
    int max_x = std::max(std::max(v[0].x(), v[1].x()), v[2].x());
    int max_y = std::max(std::max(v[0].y(), v[1].y()), v[2].y());
    
    for (int x = min_x; x <= max_x; x++)
    {
        for (int y = min_y; y <= max_y; y++)
        {
            if (insideTriangle(x + 0.5, y + 0.5, t.v))
            {
                auto [alpha, beta, gamma] = computeBarycentric2D(x + 0.5, y + 0.5, t.v);
                float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                zp *= Z;

                int cur_index = get_index(x, y);
                if (zp < depth_buf[cur_index])
                {
                    depth_buf[cur_index] = zp;

                    auto interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1);
                    auto interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1);
                    auto interpolated_texcoord = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1);
                    auto interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1);

                    fragment_shader_payload payload(interpolated_color, interpolated_normal.normalized(), interpolated_texcoord, texture ? &*texture : nullptr);
                    payload.view_pos = interpolated_shadingcoords;
                    auto pixel_color = fragment_shader(payload);

                    Vector2i vertex;
                    vertex << x, y;
                    set_pixel(vertex, pixel_color);
                }
            }
        }
    }

}

Blinn-Phong模型，计算漫反射、环境光反射、高光反射的值。

normal

Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = payload.color;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = payload.color;
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    Eigen::Vector3f result_color = {0, 0, 0};
    for (auto& light : lights)
    {
        Eigen::Vector3f light_vector = (light.position - point).normalized();
        Eigen::Vector3f view_color = (eye_pos - point).normalized();
        Eigen::Vector3f half_vector = (light_vector + view_color).normalized();
        Eigen::Vector3f n_vector = normal.normalized();

        float r2 = (light.position - point).dot(light.position - point);

        // cwiseProduct是逐元素相乘
        Eigen::Vector3f la = ka.cwiseProduct(amb_light_intensity);
        Eigen::Vector3f ld = kd.cwiseProduct(light.intensity / r2) * std::max(0.0f, n_vector.dot(light_vector));
        Eigen::Vector3f ls = ks.cwiseProduct(light.intensity / r2) * std::pow(std::max(0.0f, n_vector.dot(half_vector)), p);
        
        result_color += la + ld + ls;
    }

    return result_color * 255.f;
}

phong

纹理贴图同上

if (payload.texture)
{
    // TODO: Get the texture value at the texture coordinates of the current fragment
    return_color = payload.texture->getColor(payload.tex_coords.x(), payload.tex_coords.y());

}

![texture (2)](/images/Graphics/Shader/texture (2).png)

凹凸效果和位移贴图待更新…

Sharing is caring!