Geometry

---

几何的表示方法可以分为两类：隐式几何（explicit）、显式几何（implicit）。

隐式几何

缺点：很难通过表达式看出是什么图形，难以描述复杂形状

优点：容易判断一个点与物体的位置关系（内外上），易于处理拓扑变化、做光线和表面的相交。

例子：

• 代数曲面（Algebraic Surfaces）

  只能用代数方程表达一些简单的形状，却无法处理复杂的图形。

• CSG(Constructive Solid Geometry)

  布尔运算，采用集合的交并差运算思想。

• 距离函数（Distance Functions）

  距离函数SDF：Signed Distance Function

  SDF = 0：位于物体表面

  SDF > 0：位于物体外部

  SDF < 0：位于物体内部

  Question：如果将图片A和图片B混合，A中灰色物体占1/3, B中灰色物体占2/3，中间状态是什么样？

  Answer：如果直接线性混合，会出现1/3黑色物体、1/3灰色物体、1/3没有物体，过度会很生硬。

  如果构造SDF，边界(SDF = 0)处于图片中间，可以得到平滑的融合效果。

  

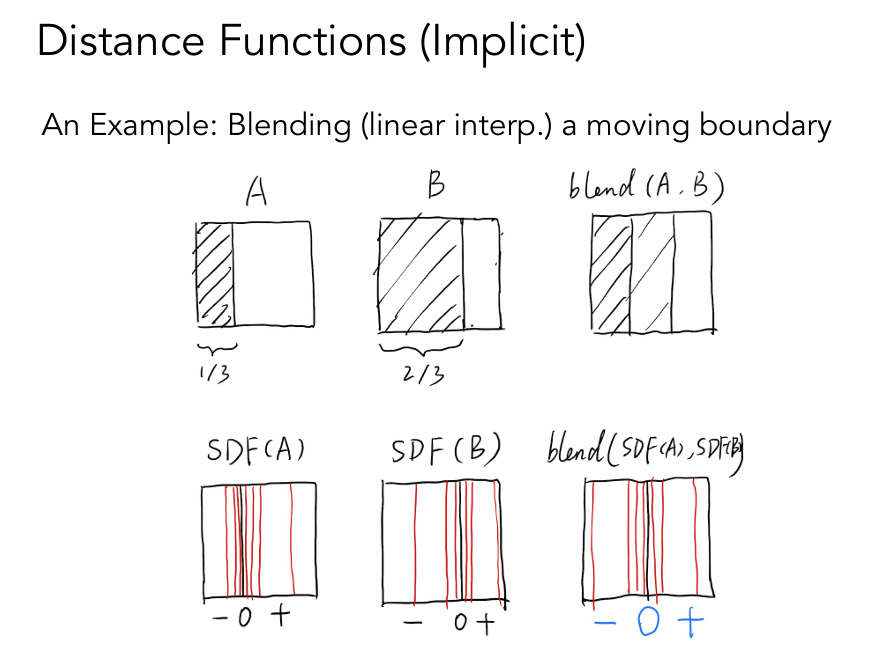
  使用网格存储距离信息，网格值为0的地方是物体表面，在地理中称作等高线。

  

• 分型

  描述具有自相似形的物体，雪花、微生物。

显式几何

缺点：难以判断某点与物体的位置关系

例子：

• 点云(Point Cloud)

  除了原始数据很少被使用，密度低时无法成面

• 多边形网格

• Wavefront Object File（.obj）格式

  描述立方体的一堆点、法线、纹理坐标及他们之间的关系

---

贝塞尔曲线

曲线一定要经过起始点p0到终止点p3，且切线为p0p1方向、p2p3方向。

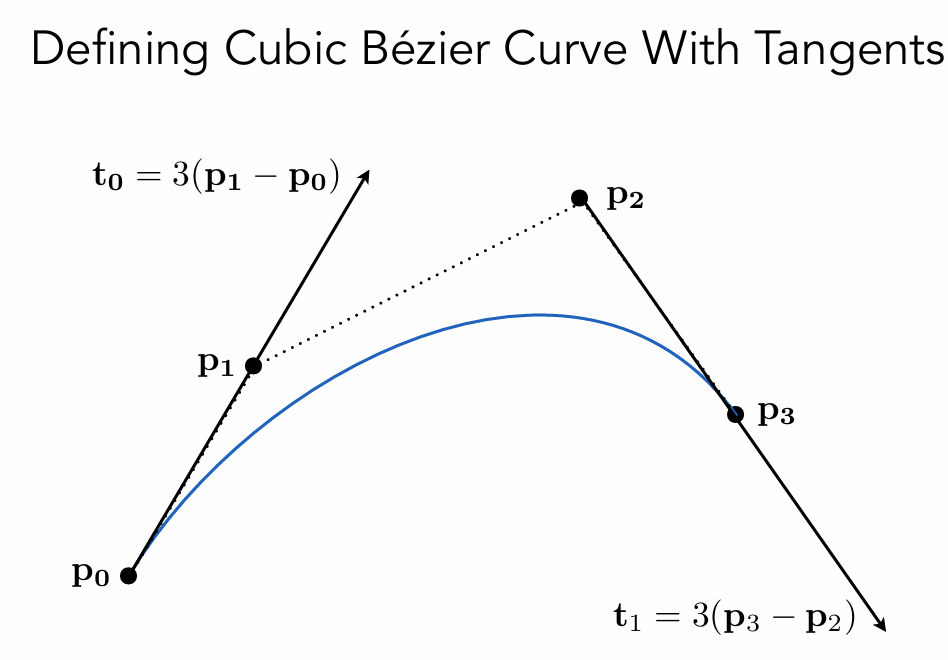
在b0 b1上找一点t 同理其他两条边，连接后变成3个点，找到b30点和该点切线

迪卡斯特里奥算法

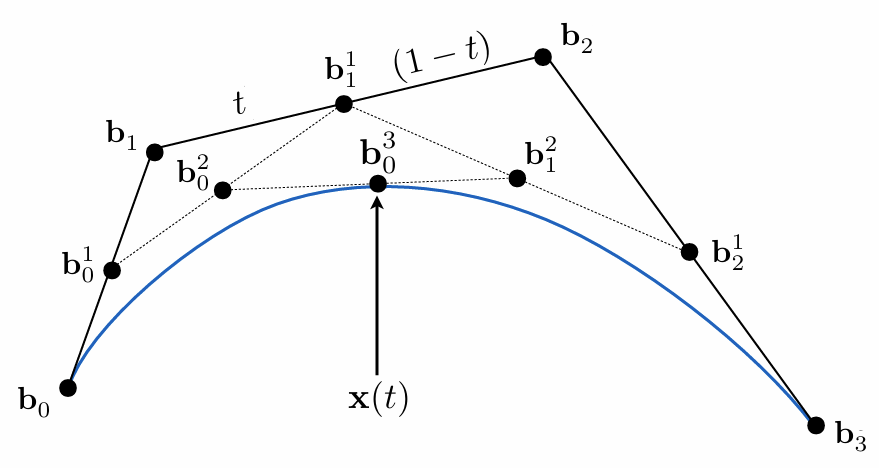
类似二项式的展开，起点系数为(1 - t)

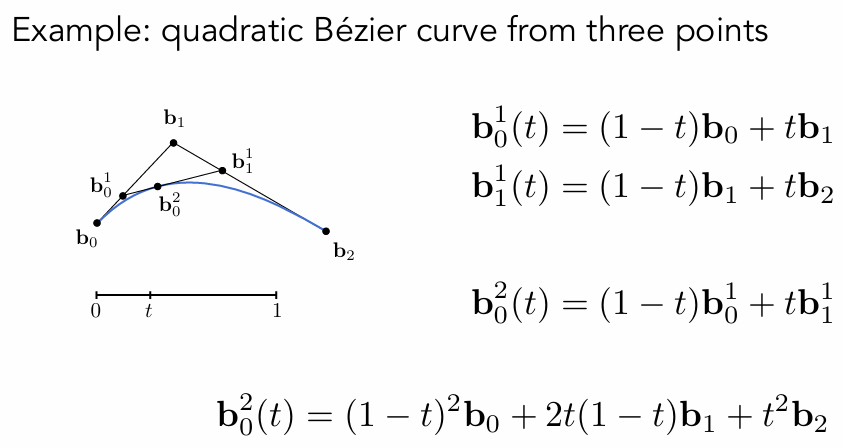
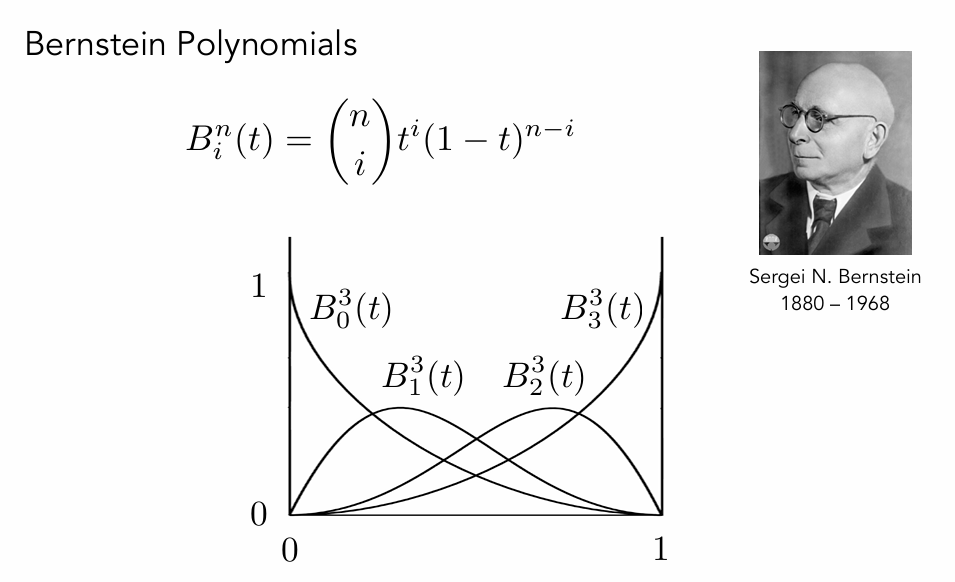
但是当n = 10时，会很难通过点去控制每条曲线，所以引出逐段贝塞尔曲线。

像是Photoshop中的钢笔工具一样，当两个点的距离相等和斜率相同时两条曲线连续。

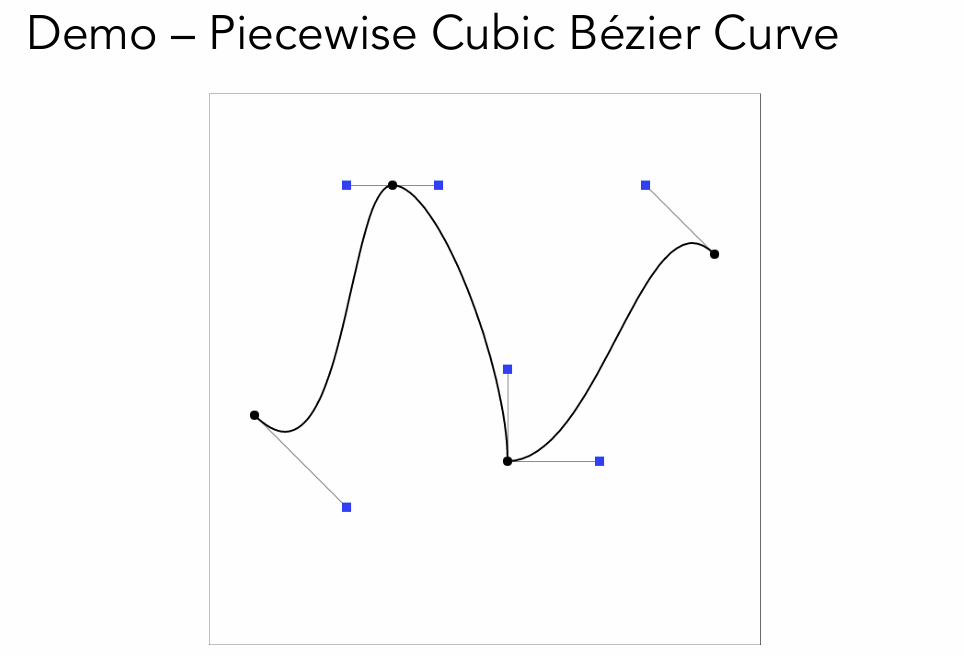
性质：

• 规定了起点和终点 t = 0一定在起点 t = 1一定在终点

• 起点终点的斜率确定

• 对贝塞尔曲线的仿射变换可以用在控制点上，对控制点进行仿射变换后，再重新画出贝塞尔曲线就可以了。（仿射变换可以，但是投影不可以）

• 凸包性质：贝塞尔曲线会在控制点形成的凸包内。

样条曲线（Splines）

B-Splines（B样条）

• 对贝塞尔曲线的一个扩展。

• 局部性：贝塞尔曲线如果动一个控制点，整个贝塞尔曲线都要进行变换，比较麻烦，B样条则不需要。

---

贝塞尔曲面

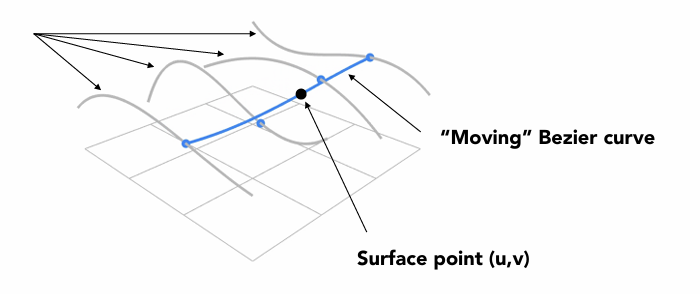
对于曲线只有一个参数t，但是对于面来说，有u和v在[0, 1]区间上。

规定了4 x 4的控制点，利用u参数得到4个蓝色点，再利用v参数得出哪个点。遍历所有的u、v可以得到一个贝塞尔曲面。

几何处理

曲面细分（Mesh Subdivision）

将模型的面分为更多小的面，提高模型精度。

Loop细分算法

​ 将1个三角形分成4个三角形，图中新的顶点（白点）需要被更新，加权平均。

​

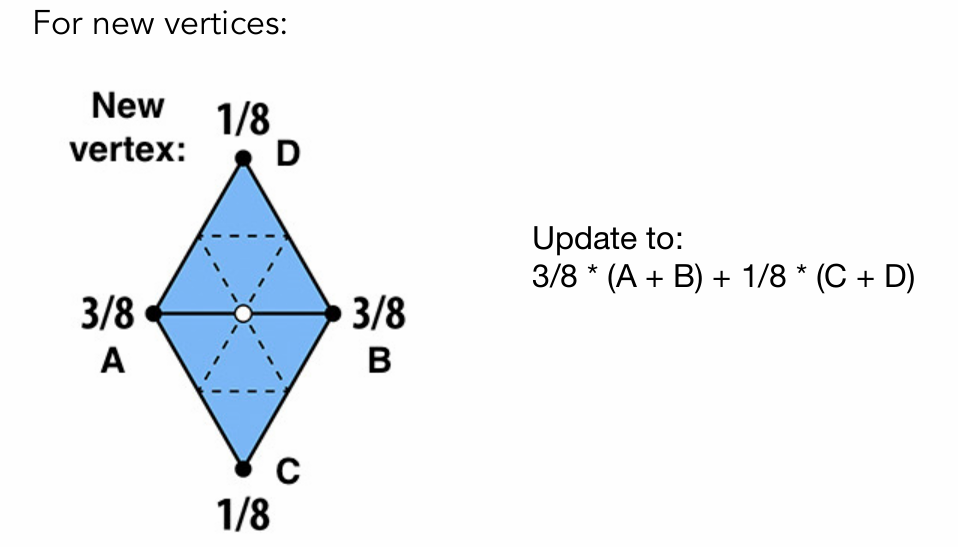
​ 旧的顶点也需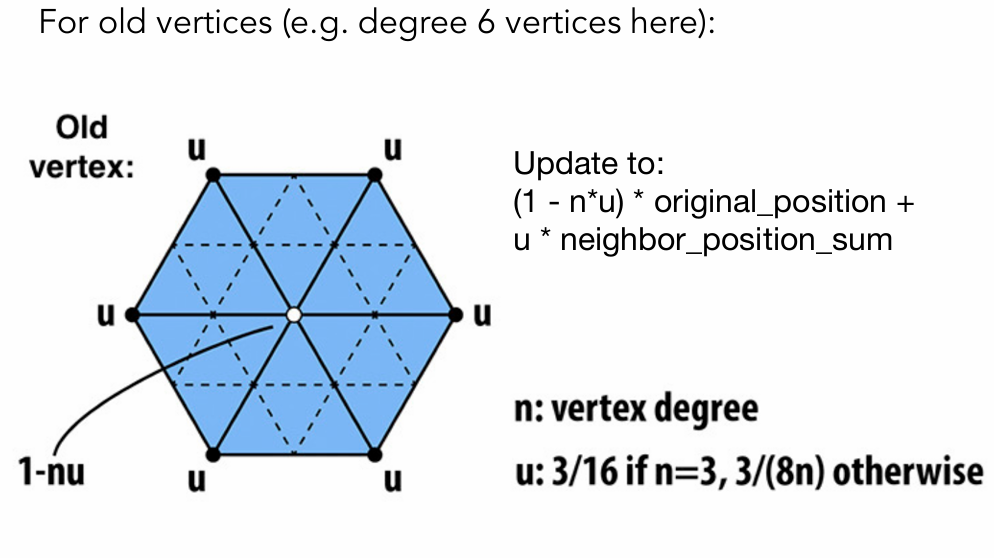要被更新，根据自己原本的位置和周围顶点的位置来做加权平均。

​ 但是loop细分只能解决三角形网格，对于四边形多边形就无法细分，所以引出Catmull-Clark。

Catmull-Clark Subdivision算法

​ 奇异点：度数 != 4的点，图中有两个奇异点和2个非四边形面。

​

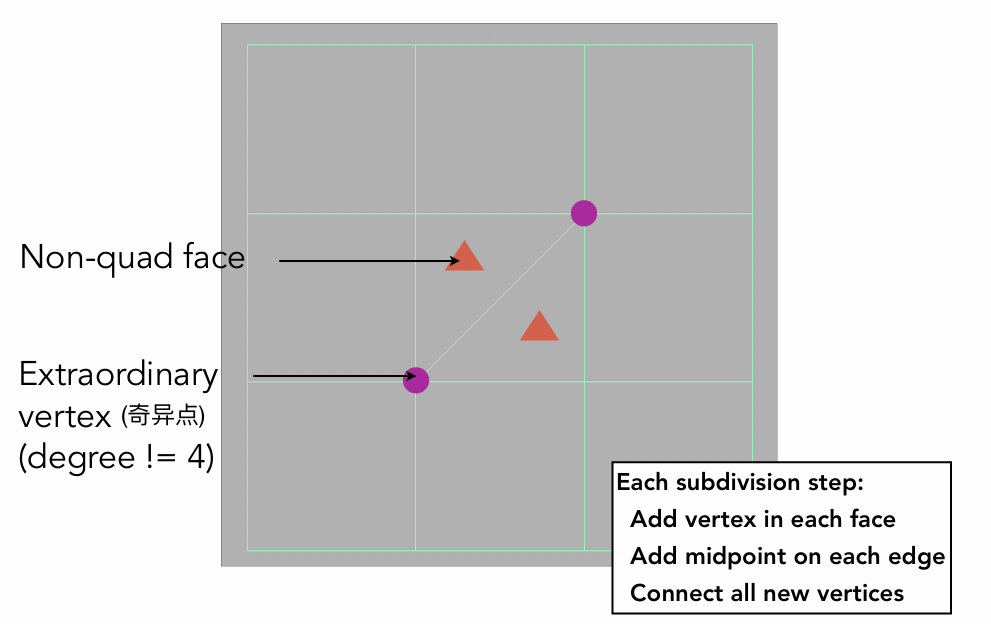
• 取每个面的一个点（比如重心）

• 取每个边的中点

• 将所有新增的点连接

​

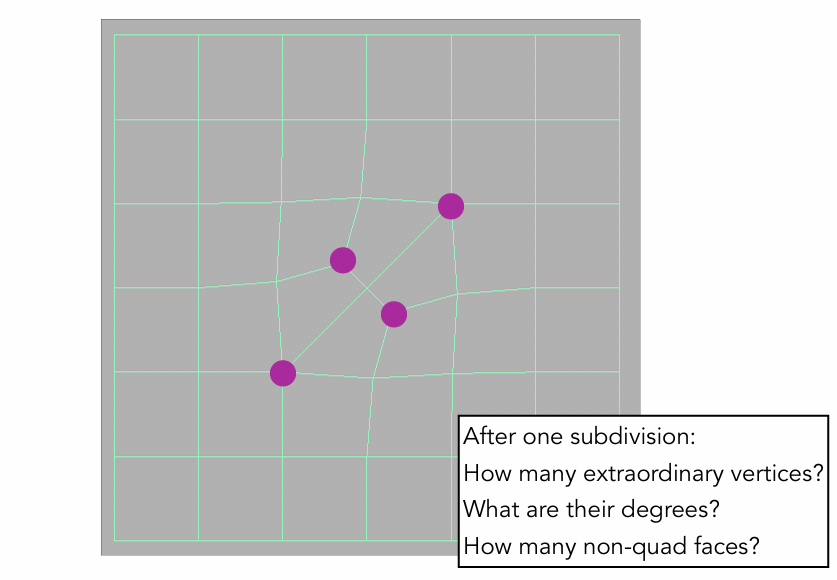
​ 细分后多出两个新的奇异点，所有非四边形面消失。（每个非四边形面会变成一个奇异点，且之后不会发生改变）

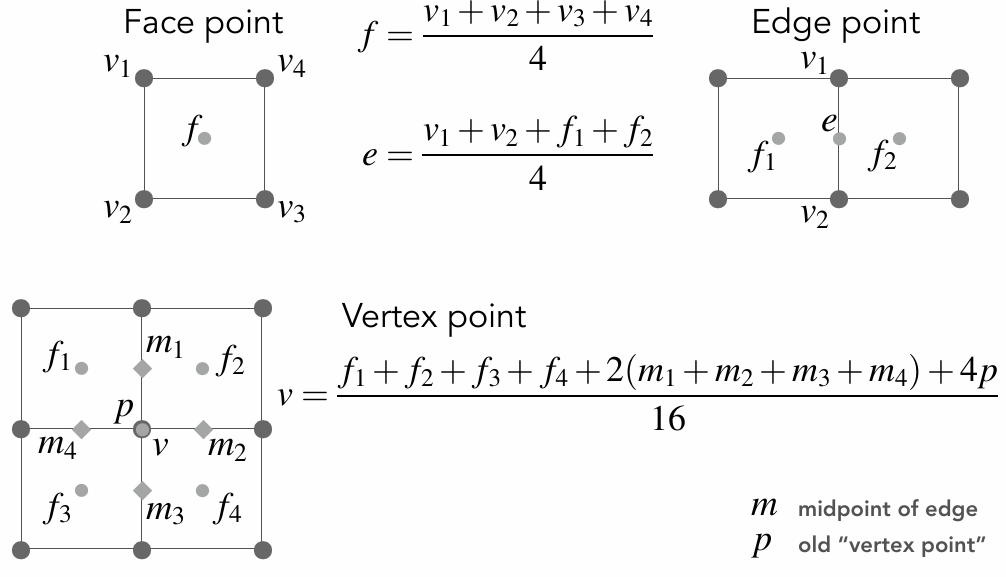
​ 对于新增的点更新规则和旧的点的更新规则

​

曲面简化 （Mesh Simplification）

降低模型精度，LOD技术。

边坍缩

想象一下将几个点捏成同一个点

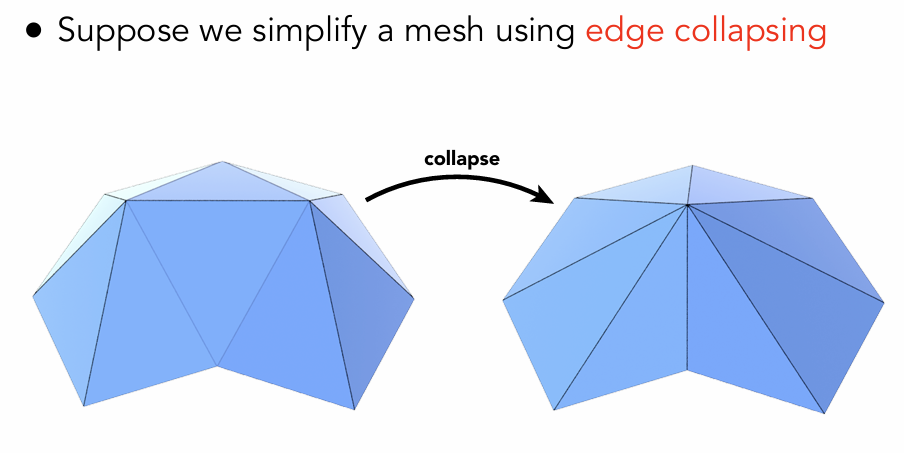
使用二次误差度量来简化曲面简化带来的误差大小

新的点应该是它相关联的面的平方和达到最小

假设坍缩每一条边，分别得出他们的二次误差，作为各自的分数；

每次都折叠分数最小的边，然后更新其他被影响边的分数；（贪心算法）

曲面规则化 （Mesh Regularization）

​ 将三角形面变得尽可能相同（正三角形），也可以提高模型效果。