RayTracing光线追踪

ShadowMapping（阴影贴图）

1. 从光源视角生成深度图，存储深度值。
2. 主摄像机渲染场景并计算阴影，与存储的深度值进行比较，如果当前点深度大于阴影贴图深度，说明该点被遮挡是阴影点；否则是光照射的点。

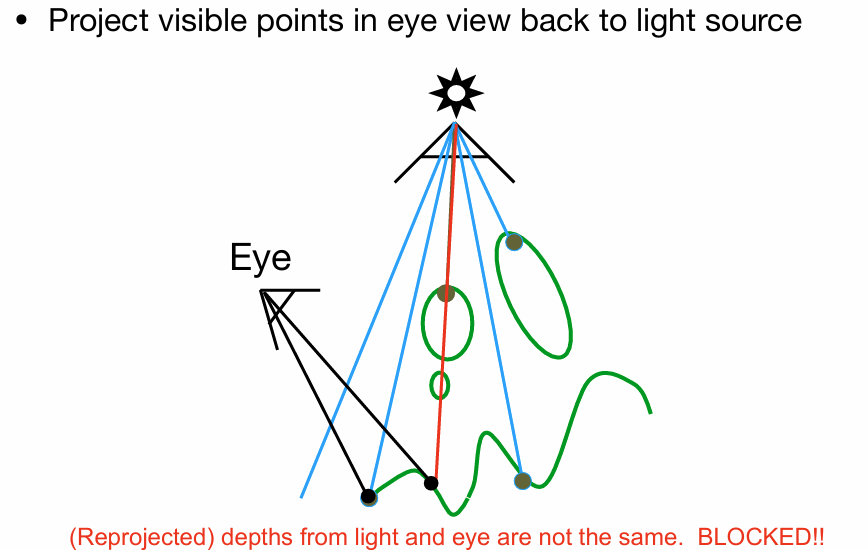
缺点：

• 生成的是硬阴影（点光源）
• 效果取决于shadowmap分辨率
• 浮点精度比较问题

由于点光源有大小，会形成如图所示的（Umbra）本影区域和半影（Penumbra）区域。所以会形成阴影的过渡。

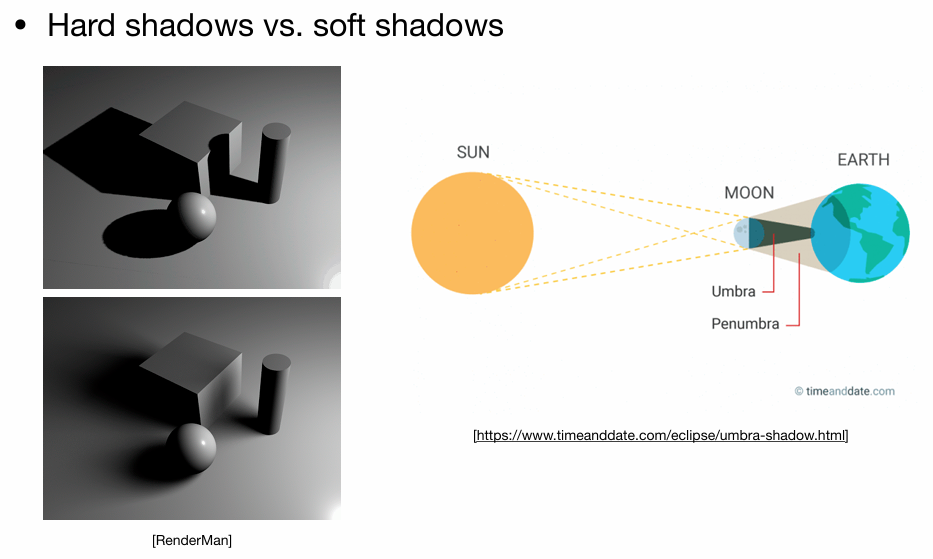
Question：为什么需要光线追踪？

Answer：光栅化难以做软阴影、难以表现光线多次弹射、光栅化（实时 游戏 快），光线追踪（离线 动画 慢）

---

光栅化：实时渲染，速度快，但是质量低。

光线追踪：离线渲染，速度慢，但是质量高。

比如疯狂动物城里的一张画面，每一帧渲染需要 10KCPU 核心小时，相当于如果只有100个CPU核，将会花费100个小时才可以渲染完成。

Whitted-Style光线追踪

关于光线3个假设：

1. 假设光线是直线的。
2. 当光线相交时，不会发生碰撞。
3. 光线从光源传播到眼睛，路径是可逆的。（互异性Reciprocity）

其中第3点意味着，当光从光源发出进行弹射后，最终进入眼睛；其实也可以认为是眼睛发射了一束感知光线进行弹射，最终回到光源。

从观察者（相机）出发，射出光线到场景中的物体表面，如果和某个物体相交，说明眼睛能看到这里。再让焦点与光线连接，判断是否有遮挡，如果没有遮挡就形成了一条有效的光路，否则为阴影。

然后对该点进行局部光照模型计算，得到该像素的颜色。

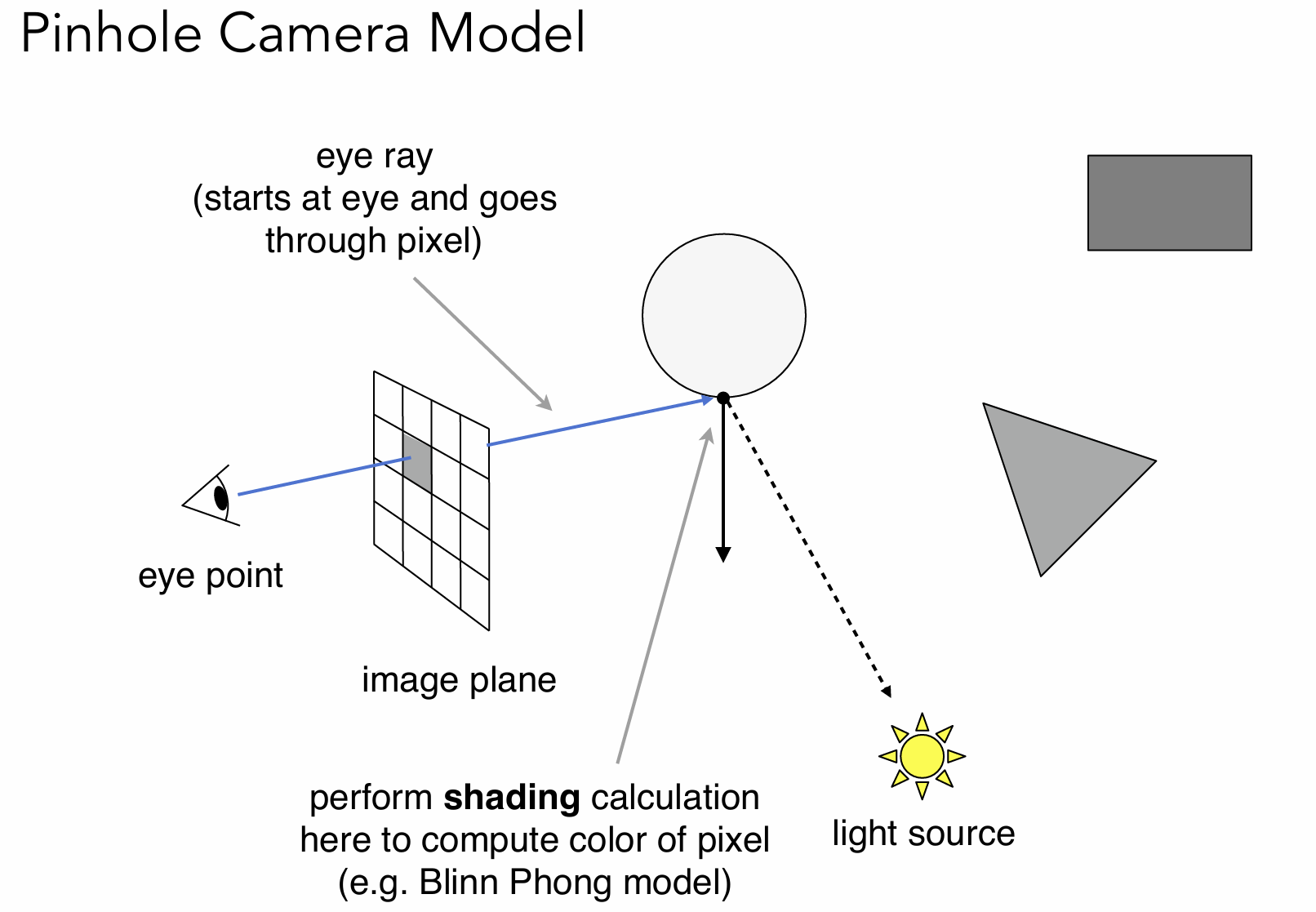
假设人眼是一个点，且光线打到物体后会进行完美的反射 / 折射。

• primary ray：人眼到第一个点的光线路径
• secondary ray：除了primary ray的其他光线
• shadow ray：光线与物体交点到光源的光线

每一个交点的颜色贡献来源于直接光照、反射方向间接光、折射方向间接光。

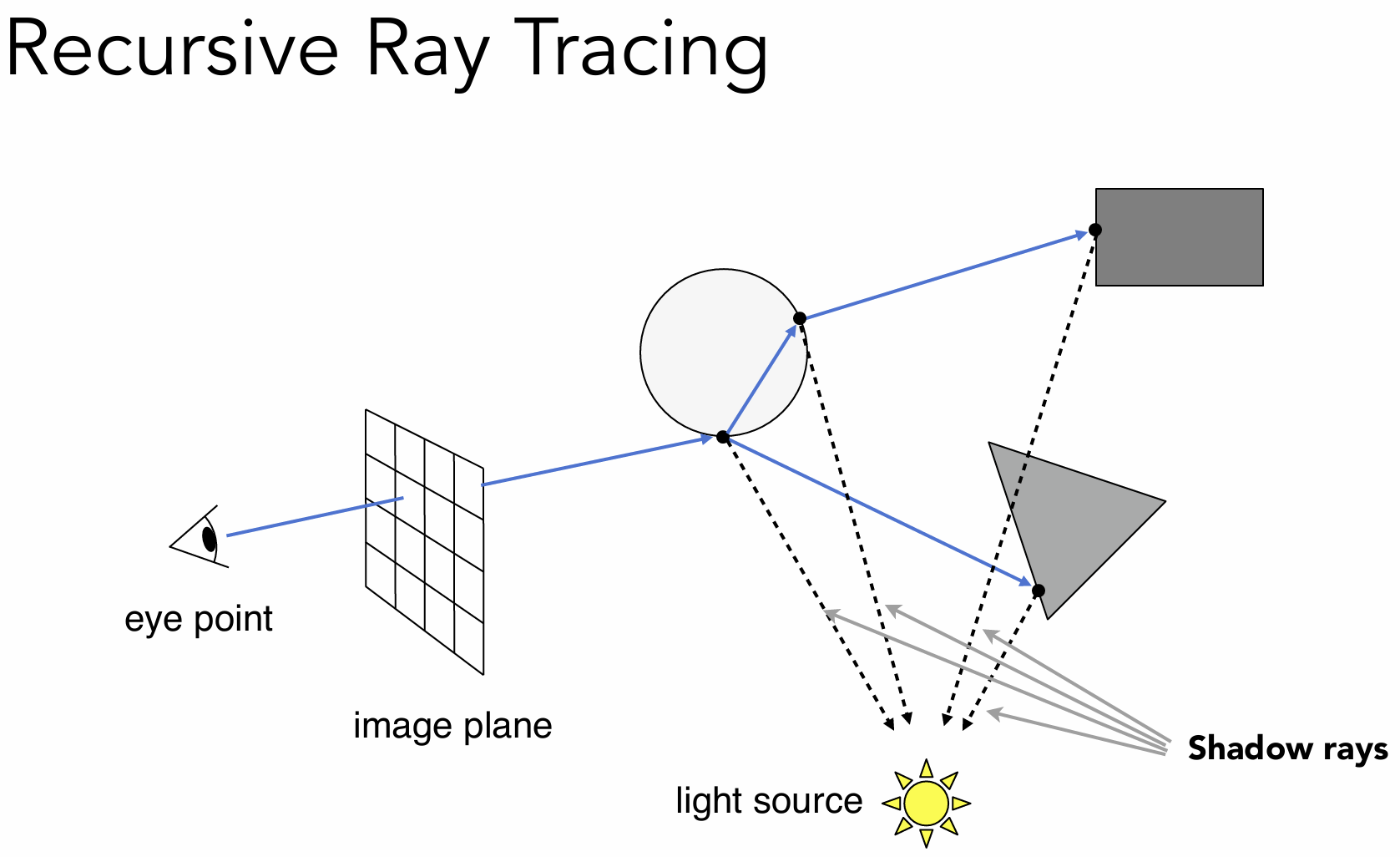
光线与物体的交点

光线的定义如下：

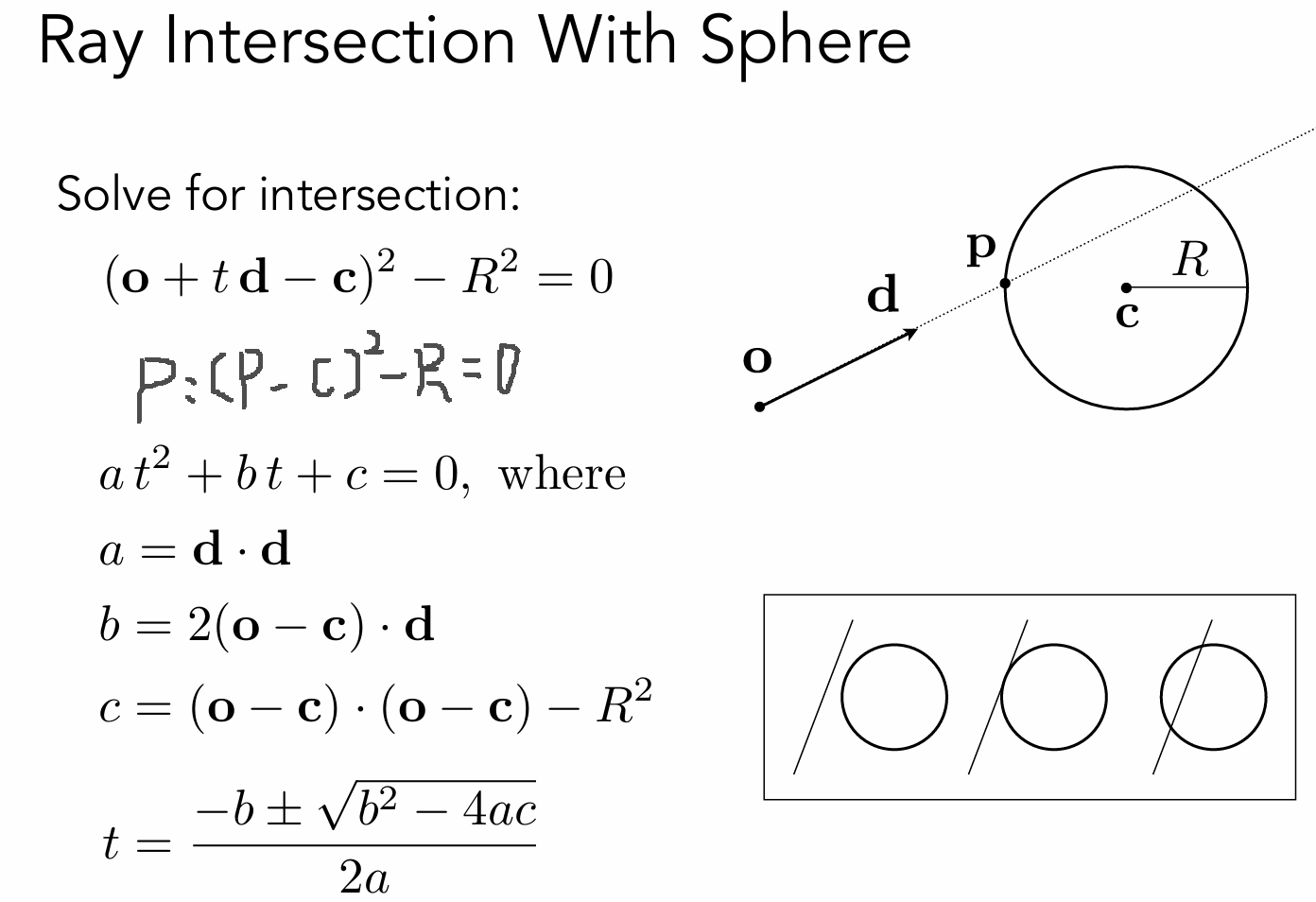
求光与球的交点，将光线公式代入到球公式中，解t。可以判断和球是否有交点，有几个交点。

如果是其他隐式几何也是同样联合光线方程。

真正在图形学中运用的其实是显式曲面，很多个三角形，因此判断的是光线与三角面的交点。与三角面的焦点可以想象成三角形在一个平面上，就变成了光线与平面的交点了。

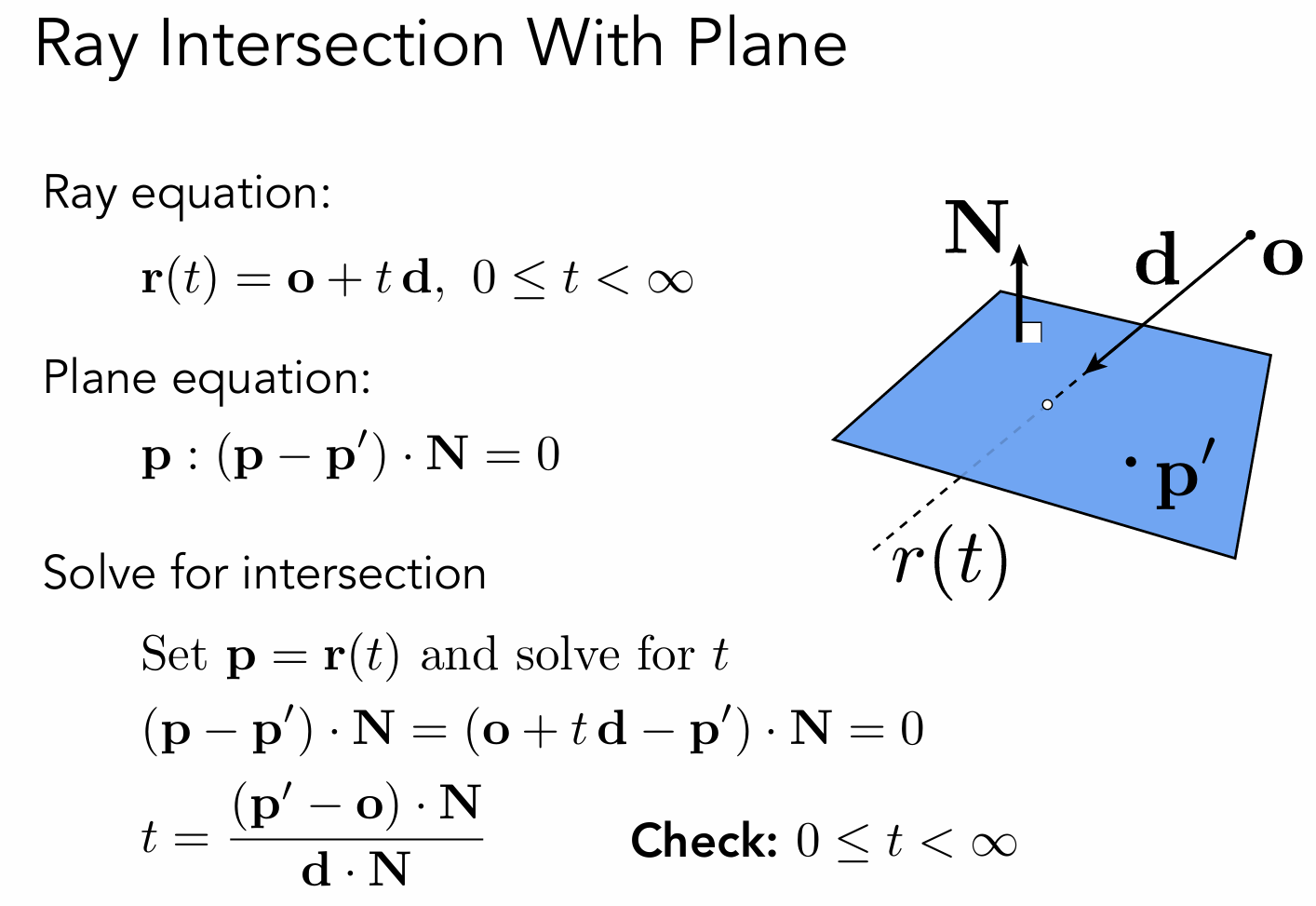
光线与平面的交点假设是p‘，那么交点与平面上任何一点p的连线，将会与N（平面的法线）垂直。

之后再判断交点是否在三角形的内部。

但是这样一个个计算太麻烦了，于是有了更方便地方法——Möller–Trumbore算法

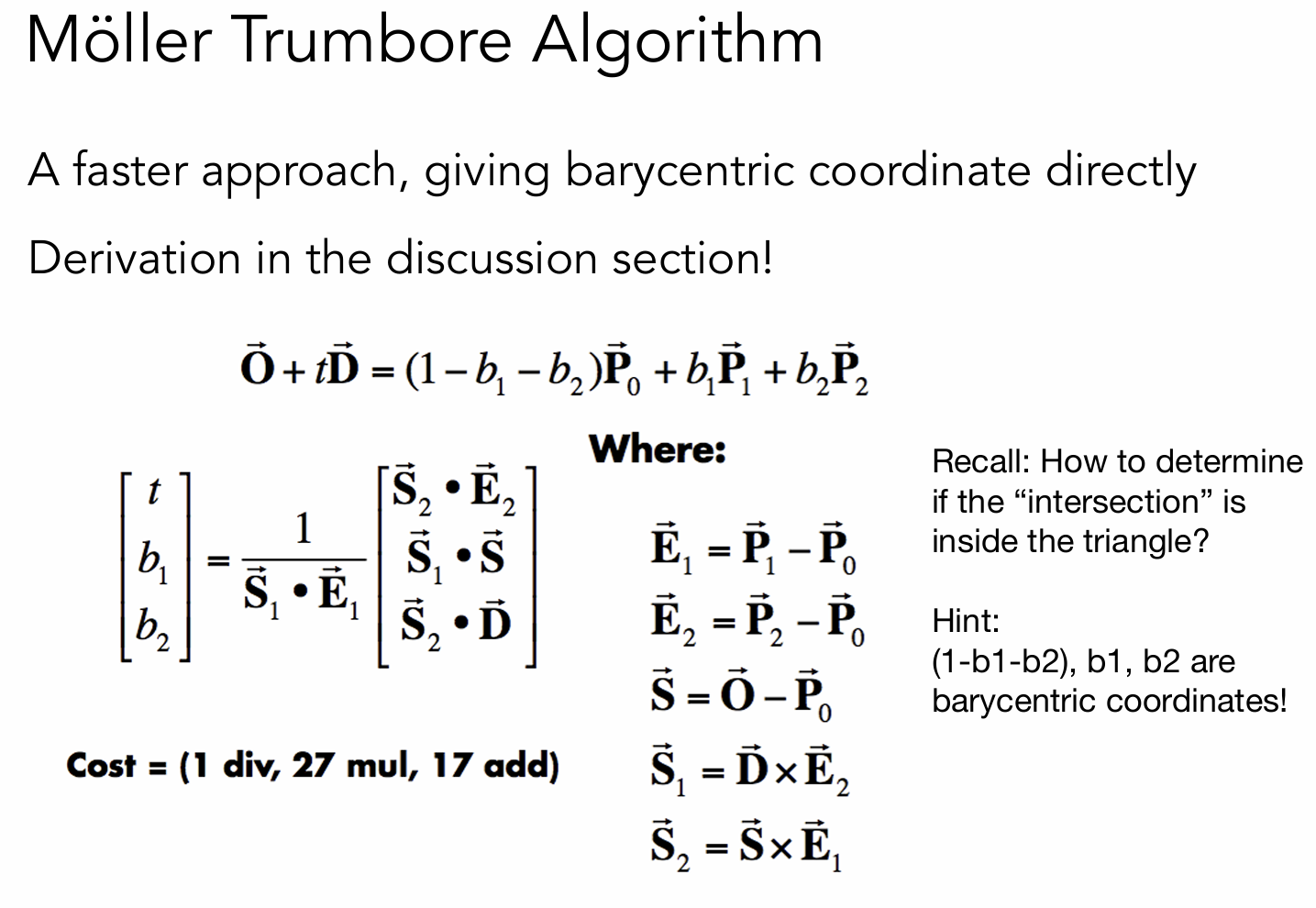
Möller–Trumbore

利用向量的外积和重心坐标来计算是否相交，大大的提高了效率。

---

在光线追踪中，光线与场景的相交检测是最核心的计算之一。简单的光线相交检测对于每一道光线需要逐一检查是否与每一个物体相交，会遍历每一个三角形进行相交测试，找出离光线最近的交点（最小t值）。但是当场景变得复杂时，三角形数量会变多，使得计算开销增加。

所以会使用一些加速结构（包围盒树、八叉树等）来减少三角形数量，使得光线与场景的相交测试只需要在较小的区域内执行，而非全部三角形。

Bounding Volumes

如果一个光线连包围盒都碰不到，也绝对不会碰到包围盒里的物体。

轴对称包围盒：将长方体用3对不同的平面包围住，任何一对平面都与x轴y轴z轴垂直，所以称为AABB包围盒。

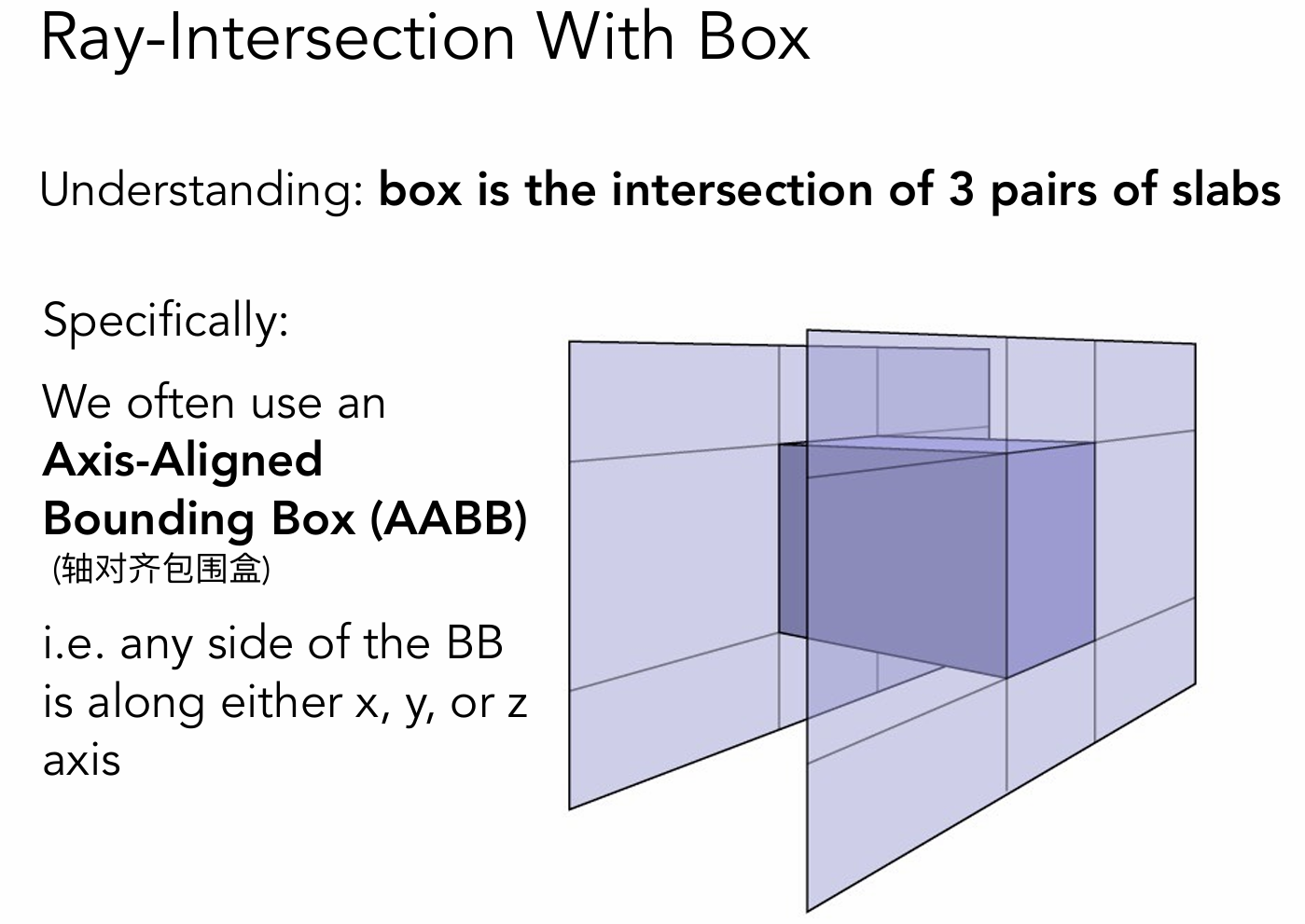
下图为光线穿过包围盒的3个对面所经历的时间，取这3个时间的交集，就是光线在包围盒里的时间段。

• 进入包围盒：进入所有对面

  $$ 最晚进入盒子的时间：t_{enter} = max\{t_{min}\} $$

• 离开包围盒：离开任一对面

  $$ 最早离开盒子的时间：t_{exit} = min\{t_{max}\} $$

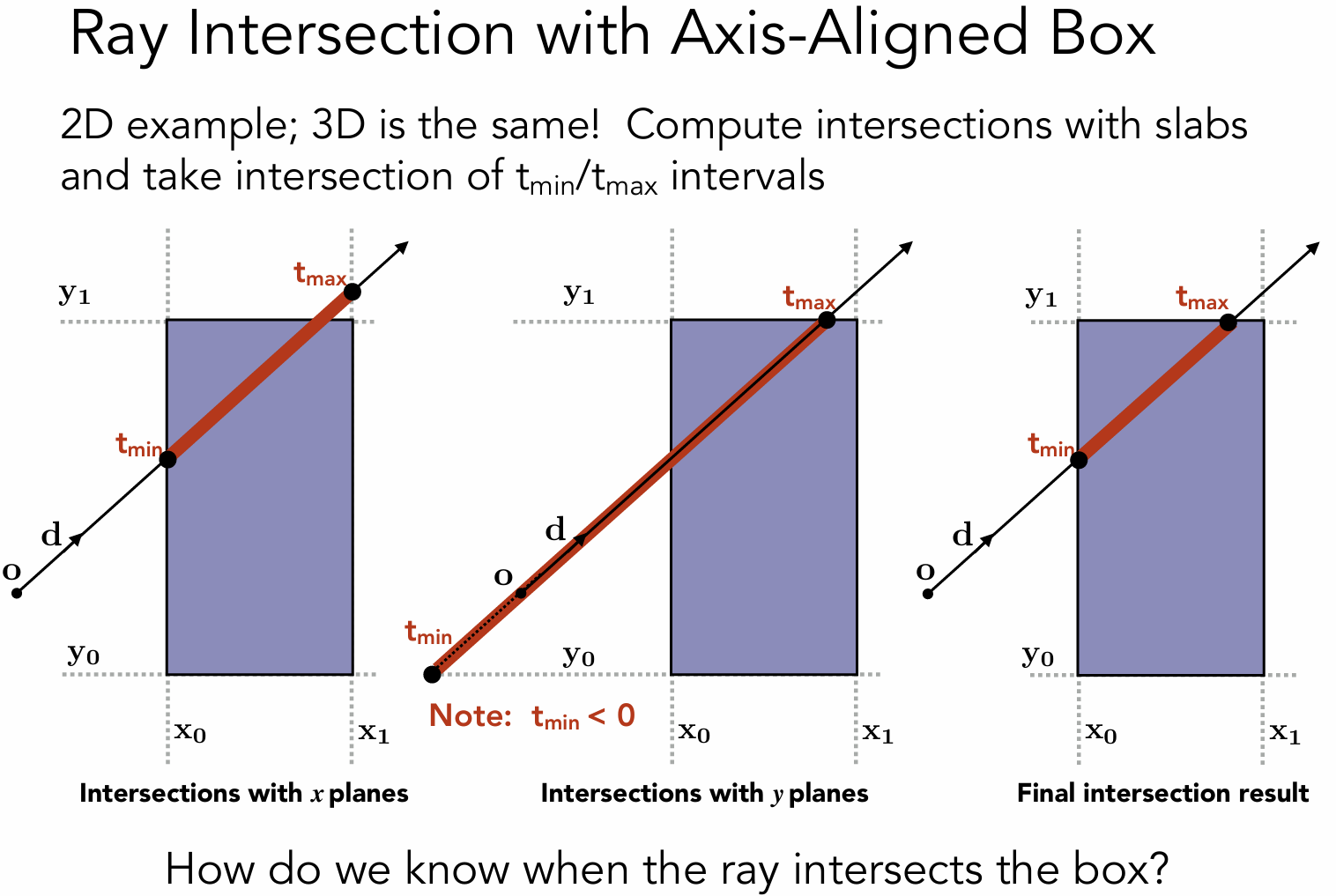
然而光线并不是直线，光线是一条射线，所以要判断t是否为正数。

当离开的时间<0时，说明盒子在光线的背后；当离开的时间>=0，进入的时间<0，代表光线起点在盒子里面。

为什么轴对称包围盒可以提高效率，因为计算公式变得简洁了很多。

$$ t = \frac{(p' - o)·N}{d·N} \qquad t = \frac{p'-o_x}{d_x} $$